专栏文章

【附代码】NOIP2025的组题确有问题？由 S->NOIP 的成绩散点图统计分析

炸炸鸡块君
科技·工程参与者 128已保存评论 136

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
136 条
当前快照
1 份
快照标识符
@mjbosxzl
此快照首次捕获于
2025/12/19 01:01
2 个月前
此快照最后确认于
2026/02/19 01:27
8 小时前
查看原文

概述

NOIP 2025 刚刚考完的时候，大家都说题目难度很大，我当时（作为教练）还觉得问题不大，毕竟难是大家都难。后来微信上悲报频传，才意识到大事不妙。
之后看了今年的题目和网上评价，逐渐意识到今年的问题可能不是难（当然难度也是问题），而是区分度可能有问题，对中等分段的学生很可能比往年更加随机区分（推测是 T2 容易吸引中等略偏上学生容易 all in 进去、而中等偏下学生更倾向于打暴力）。
于是为了验证这个猜想，我选取了几个代表省份，画了参加今年 NOIP 考生的成绩散点图，具体包括了省一人数大于 100100 的所有省份（浙江、江苏、广东、山东、四川），再加上北京和重庆。然后和 GPT 交流了一下，用斯皮尔曼等级相关系数来定量刻画了某年 CSP 与 NOIP 成绩的相关性。文章结尾会附上代码和运行说明。

从首都看起

以我所在的北京为例，20252025 年的 CSP 和 NOIP 成绩散点图如下：
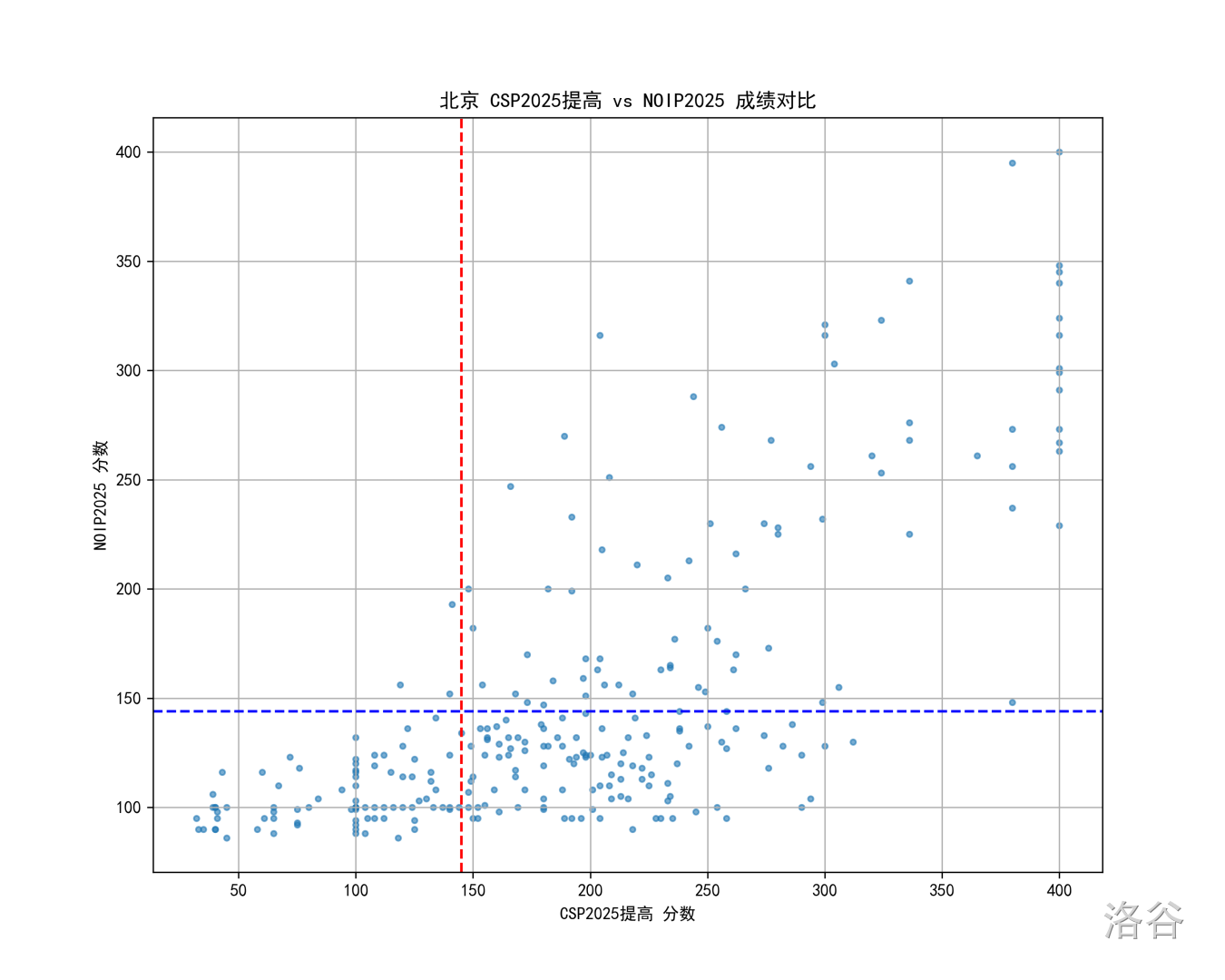
图中每个点是一个考生，红线和蓝线分别是 CSP 和 NOIP 的一等线。
对这张图，我们有如下几个印象：
  • 高分段的选手（CSP 300+ 和 NOIP 250+）受影响不大，牛的选手就是在各种题面前都很牛；
  • 低分段的选手（CSP 150-）从省一角度看区分度是符合预期的，即几乎所有未获得 S1 的学生也打不到 NOIP 省一；
  • 中分段的选手（CSP 150~300）似乎出现了随机区分，我们单独看 CSP 成绩 x∈[150,200]x\in [150,200]、x∈[200,250]x\in [200,250]、x∈[250,300]x\in [250,300] 对应的三个矩形区域，甚至感觉 shuffle 一下也毫无违和感（？）。再从 NOIP 角度来看，y∈[100,150]y\in [100,150] 在 x∈[100,300]x\in [100,300] 区域的分布也似乎是大差不差的。
如此，看上去 NOIP 2025 区分度确有问题......这严谨吗？一个可能的质疑是，OI 赛制本身就有很大的不确定性，如何识别上述中分段随机区分是来自赛制特性还是题目特性？
所以一个自然的想法是，我们看看往年的情况，比如 24 年的北京 CSP 对比 NOIP 散点图：
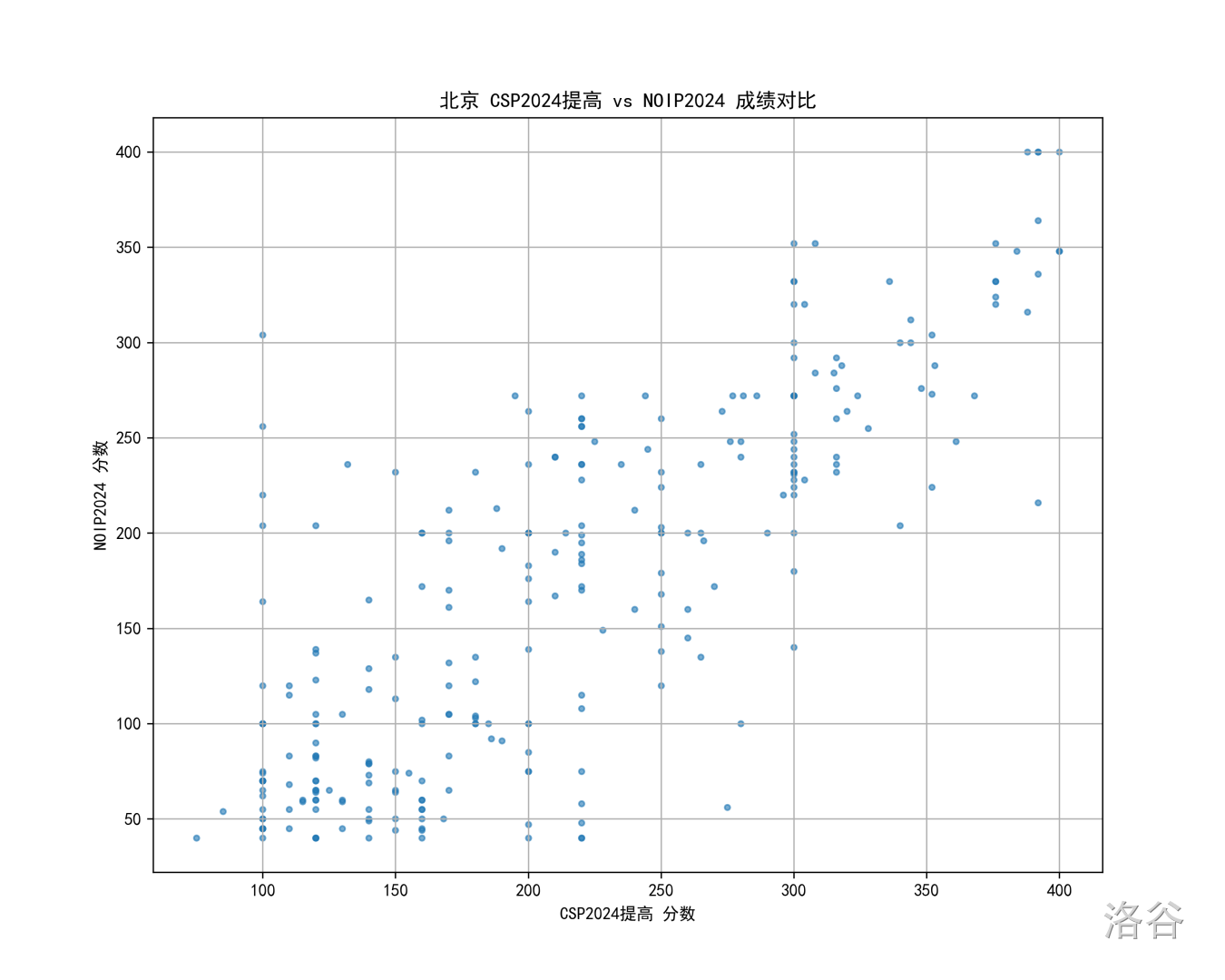
虽然人脑不能拿来拟合直线，但我好像真从上图看到线性了（
当然，细看的话会发现 x∈[200,300]x\in [200,300] 一段区分度也不太好，但这可能更多归于 OI 赛制特性，看占比的话也还是能看出 x∈[250,300]x\in [250,300] 段会更靠上一点。
插叙一句，我一直觉得 NOIP 2024 是难度、区分度、部分分三方面都做得很好的一套题，今年的题目单题质量都很好，组出来就非常不合适。一些“NOIP 应该提前承担省选作用”、“对省队选手影响不大就 OK”的观点在我看来是没道理的，一个有力的反驳就是赛制被设计成了 NOIP 400 + 省选 600 的两场比赛，这个设计预期就是 NOIP 选省一、省选选省队，4:6 的分数比例也不存在让 NOIP 承担省选功能的道理。跑题了，不继续展开了。
对比了两年的散点图，直观上确实觉得 25 的散点图，嗯，很特殊，但总归是打眼一看的印象派，我们有没有办法定量刻画一下 CSP 与 NOIP 的分数一致程度？

斯皮尔曼等级相关系数

（经过和 GPT5.2 的激烈讨论，我学到了）斯皮尔曼等级相关系数（Spearman's ρ\rho）是一种衡量两组数据排名一致程度的指标，其思想是求排名向量之间的余弦相似度（或者说夹角）。
算法大致流程是，对于 nn 个学生的 CSP 成绩 (x1,x2,…,xn)(x_1,x_2,\ldots ,x_n) 和 NOIP 成绩 (y1,y2,…,yn)(y_1,y_2,\ldots ,y_n)，首先用其该场比赛的排名替换原始成绩：
  • xi←rankx(xi)x_i\larr \mathrm{rank}_x(x_i)
  • yi←ranky(yi)y_i\larr \mathrm{rank}_y(y_i)
rankarank_a 是求一个数在序列 aa 排名中的函数，当出现分数并列的情况时，会将并列的人都赋值为并列排名的均值（如排名 33、44、55 的三人分数相同，则排名都赋为 44）。
接下来，定义：
ρ=∑i=1n(xi−xˉ)(yi−yˉ)∑i=1n(xi−xˉ)2∑i=1n(yi−yˉ)2\rho=\frac{\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)}{\sqrt{\sum_{i=1}^n (x_i-\bar x)^2}\sqrt{\sum_{i=1}^n (y_i-\bar y)^2}}
为斯皮尔曼等级相关系数，其取值范围为 [−1,1][-1,1]，值 >0>0 表示正相关，且绝对值越大相关性越强。公式中 xˉ\bar x 和 yˉ\bar y 为各自排名的平均值。
考虑 ρ\rho 为什么能反映相关性：对于两个 nn 维向量
  • X=(x1−xˉ,x2−xˉ,…,xn−xˉ)X=(x_1-\bar x,x_2-\bar x,\ldots ,x_n-\bar x)
  • Y=(y1−yˉ,y2−yˉ,…,yn−yˉ)Y=(y_1-\bar y,y_2-\bar y,\ldots ,y_n-\bar y)
则 ρ\rho 的分子是两向量点积，分母是两向量模长乘积，因此 ρ\rho 是两向量夹角的余弦值，取值范围为 [−1,1][-1,1]，取 −1-1 时两向量方向相反、取 00 时两向量夹角为 9090 度，取 11 时两向量方向相同。
于是，我统计了之前提到的大省们近三年的 CSP 与该年 NOIP 的 ρ\rho 值，结果如下：
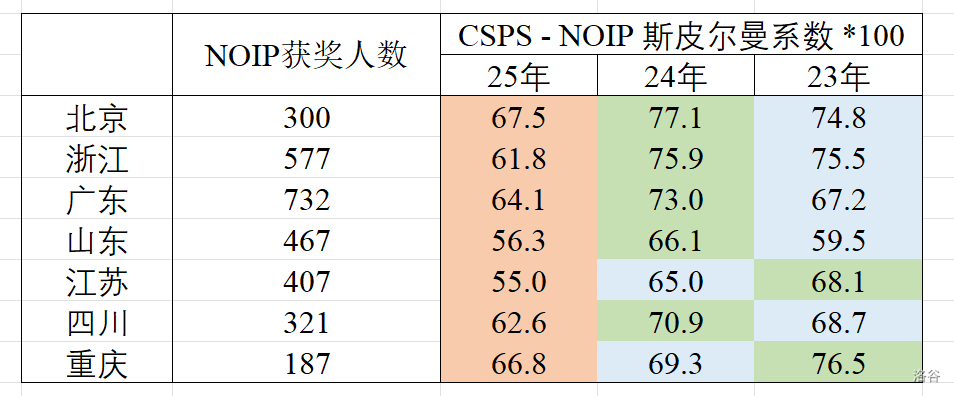
  • 表中绿、蓝、橙分别对应该省近三年 ρ\rho 值最大、次大、最小的年份，可以看出 25 年确实稳居倒数第一；
  • 一些省份（如山东）的 ρ\rho 值会整体偏低，可能是因为这些省份低分选手（CSP在一等线下的）相对多，这些选手看散点图的话 NOIP 成绩基本上随机区分的（这某种程度上是预期的，不算题目的问题），导致 ρ\rho 值降低。
  • 需要说明，我们求得的其实是 CSP 和 NOIP 效果的一致性，该值高确实能说明两边的筛选效果是一致的好，但该值低只说明 CSP 与 NOIP 筛选效果不一致、不能确定是 CSP 的问题还是 NOIP 的问题。具体到今年的情况，我只能主观心证确实是 NOIP 的问题，没法证明。

更多结果

下面提供上述其他省份的散点图，可以自行取用。

重庆

重庆要专门说几句，因为接下来大家会看到大多省份的散点图和上面北京的大差不差，只有重庆的散点图很不一样。请感受重庆的强度：

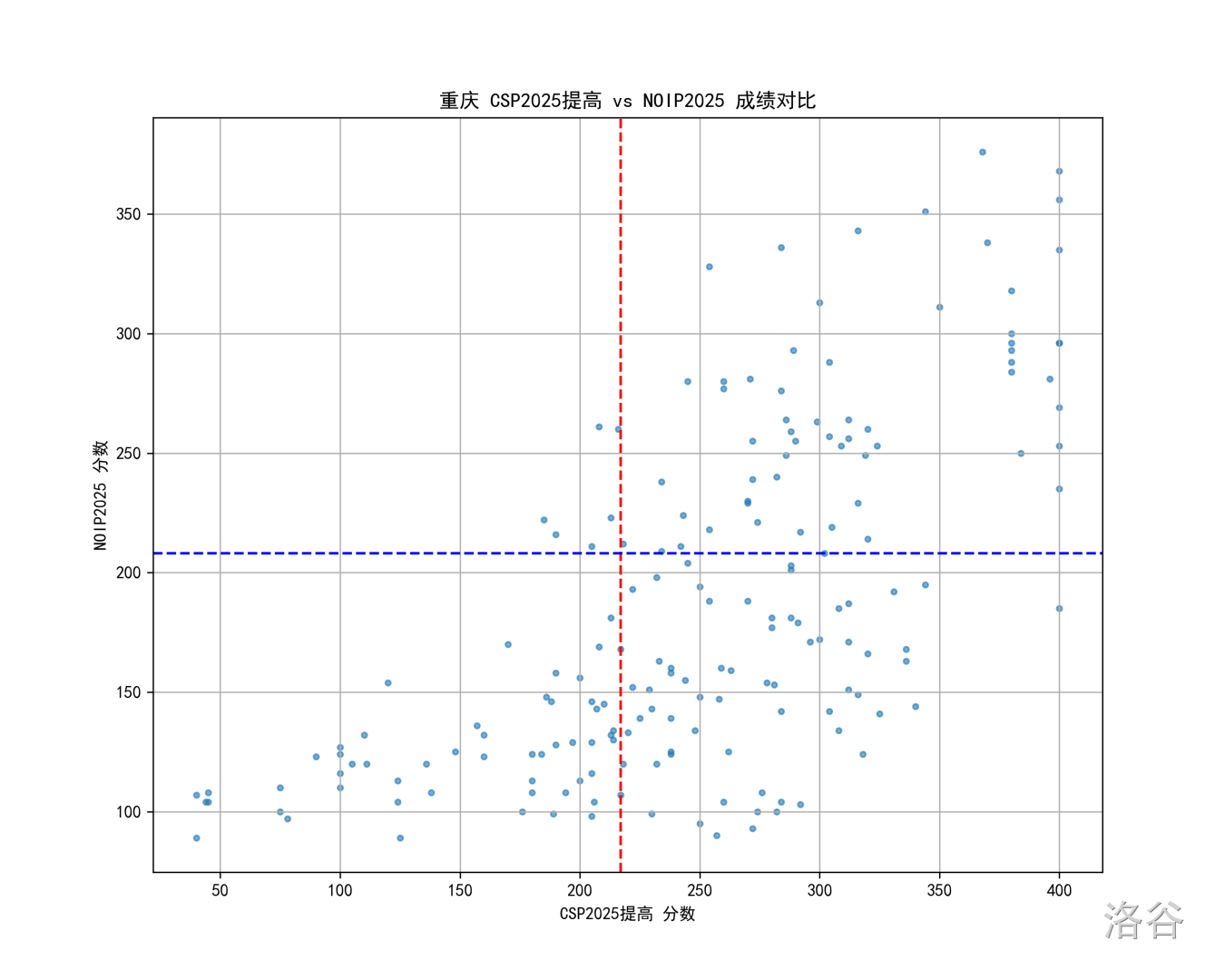
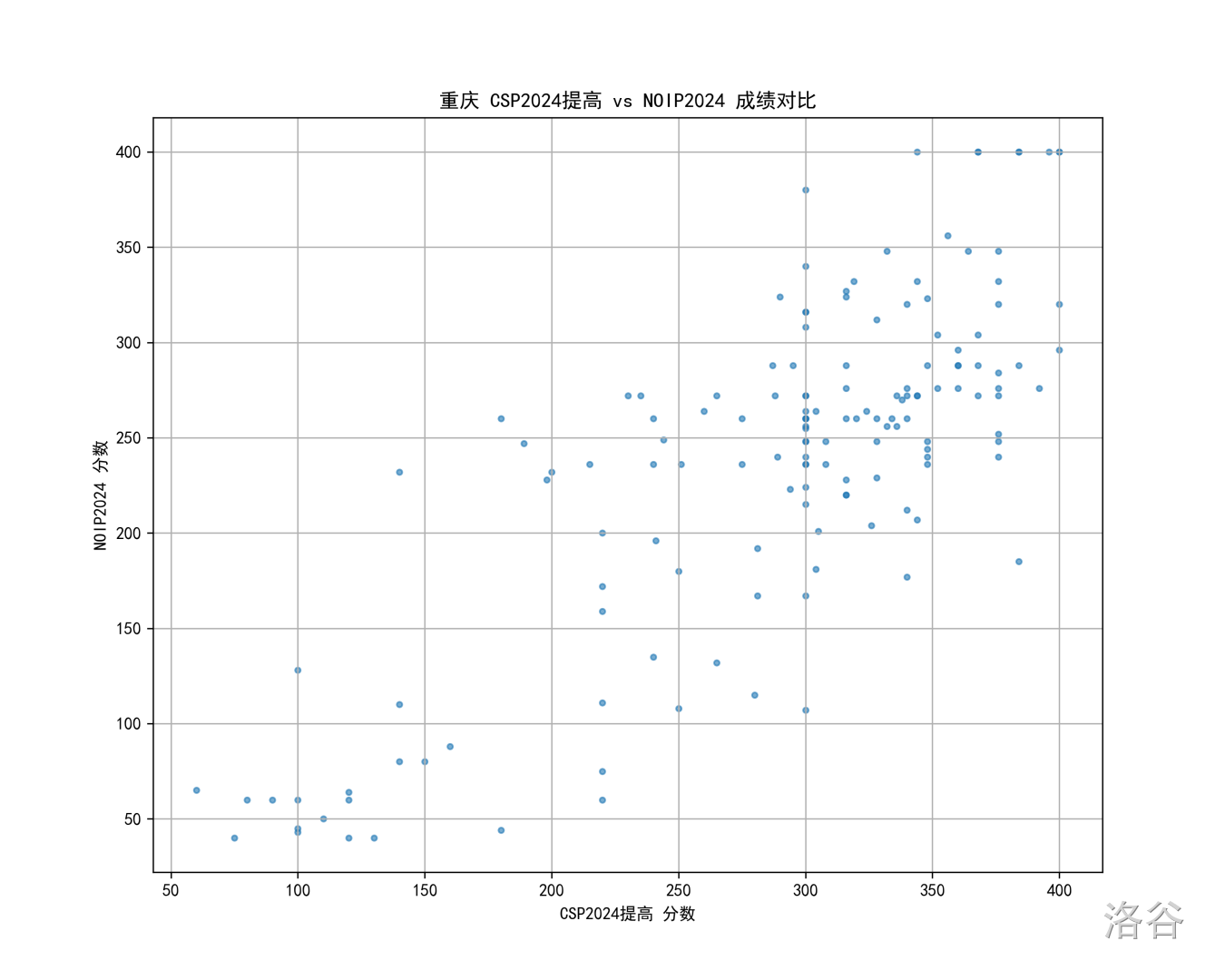
浙江

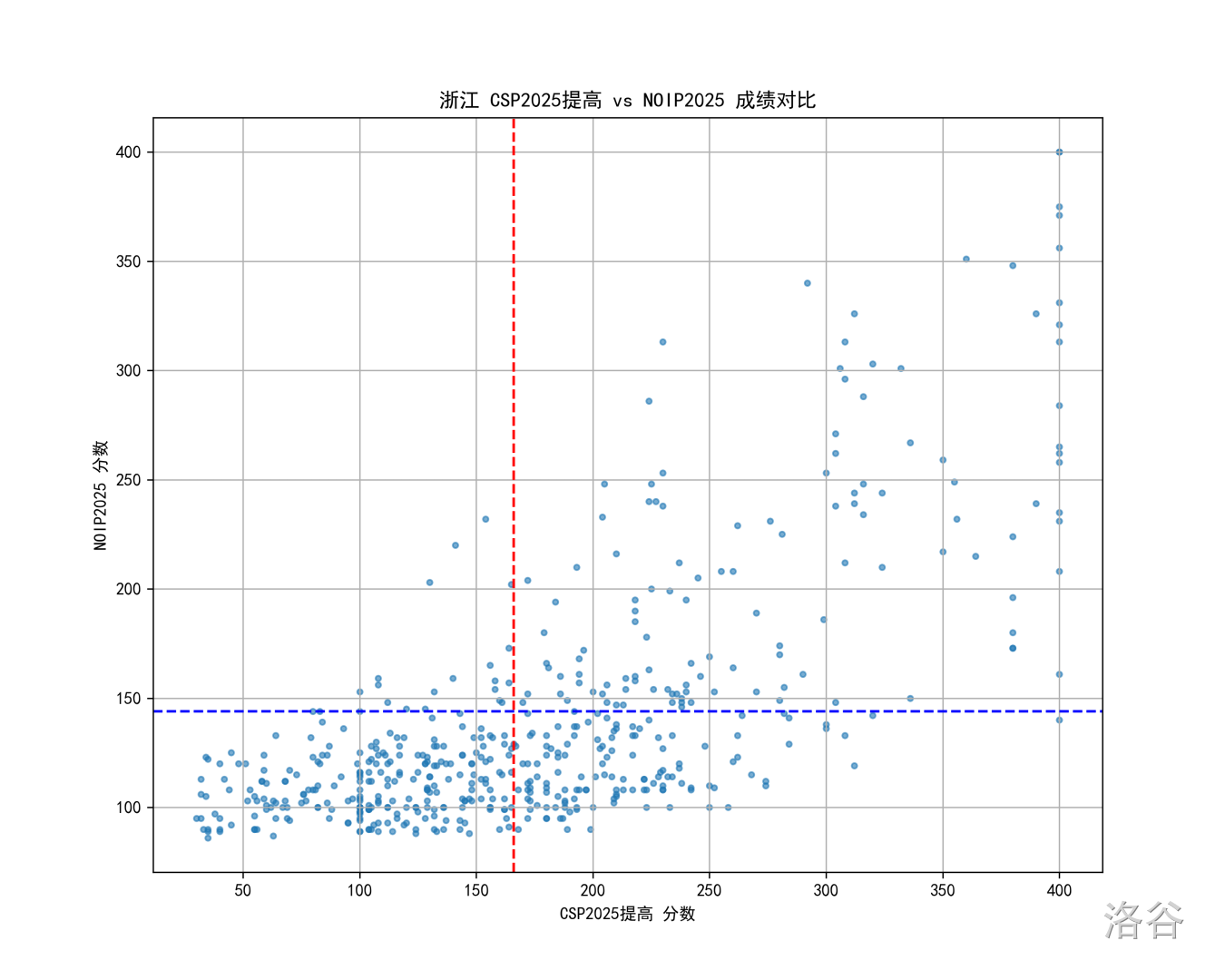
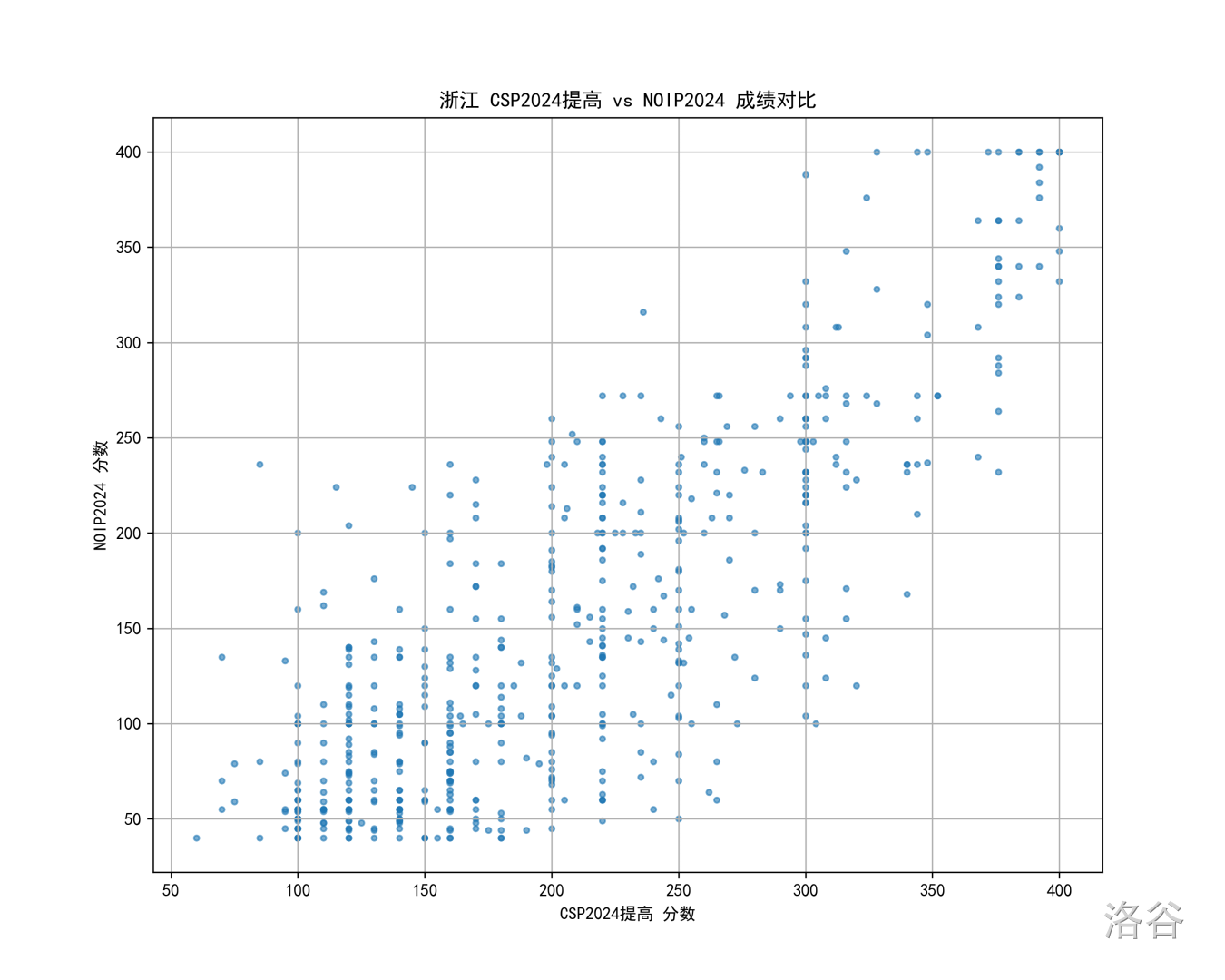
广东

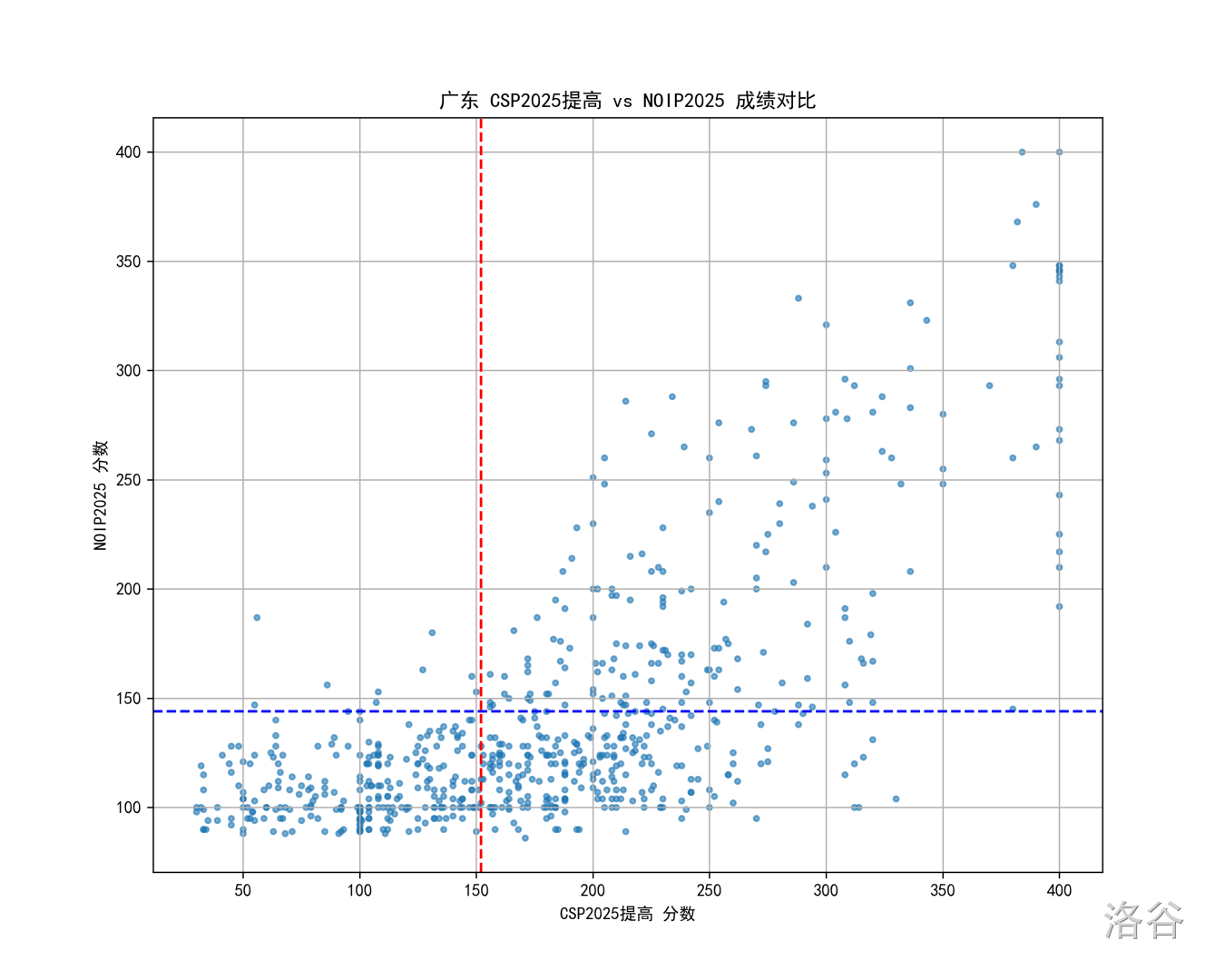
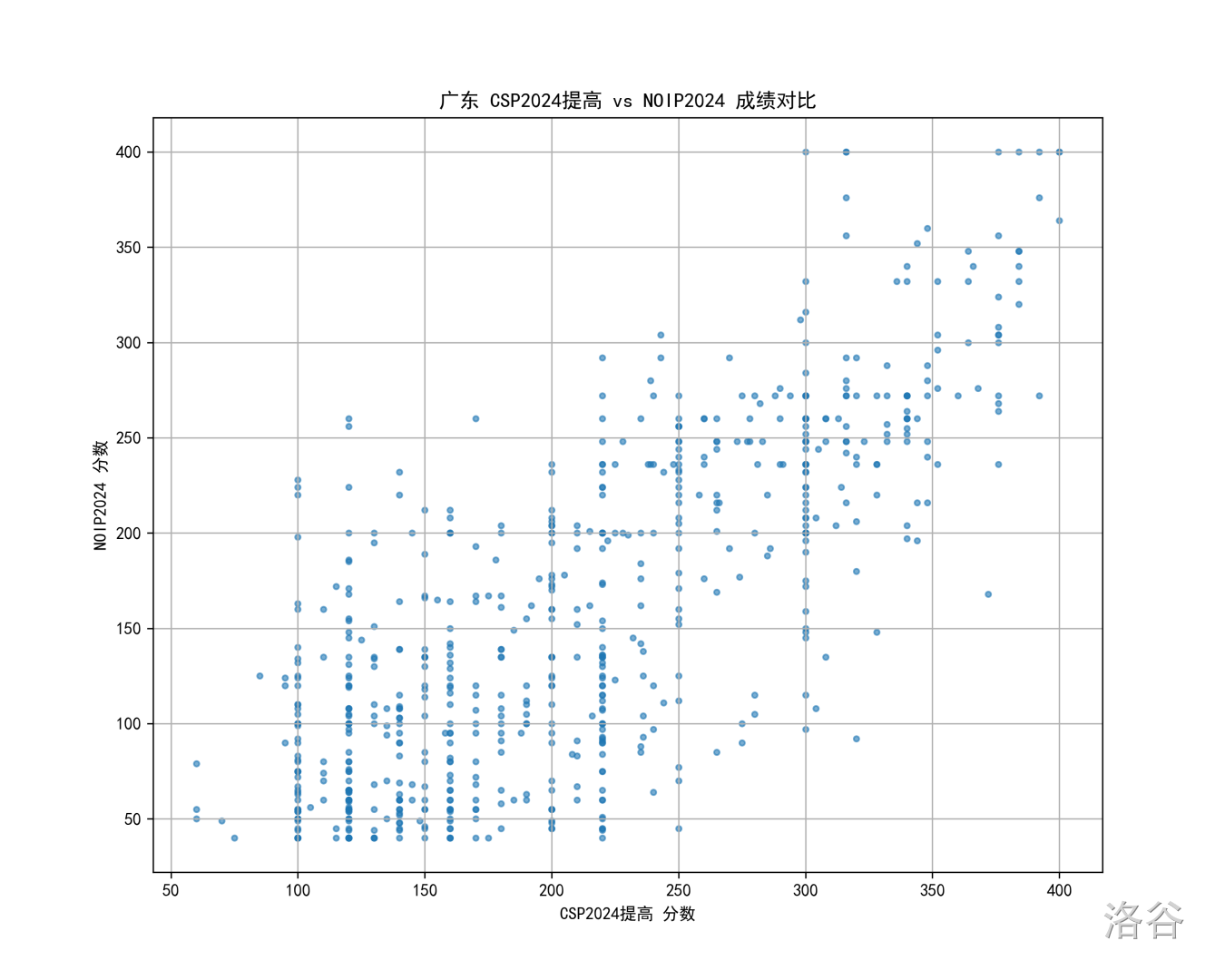
山东

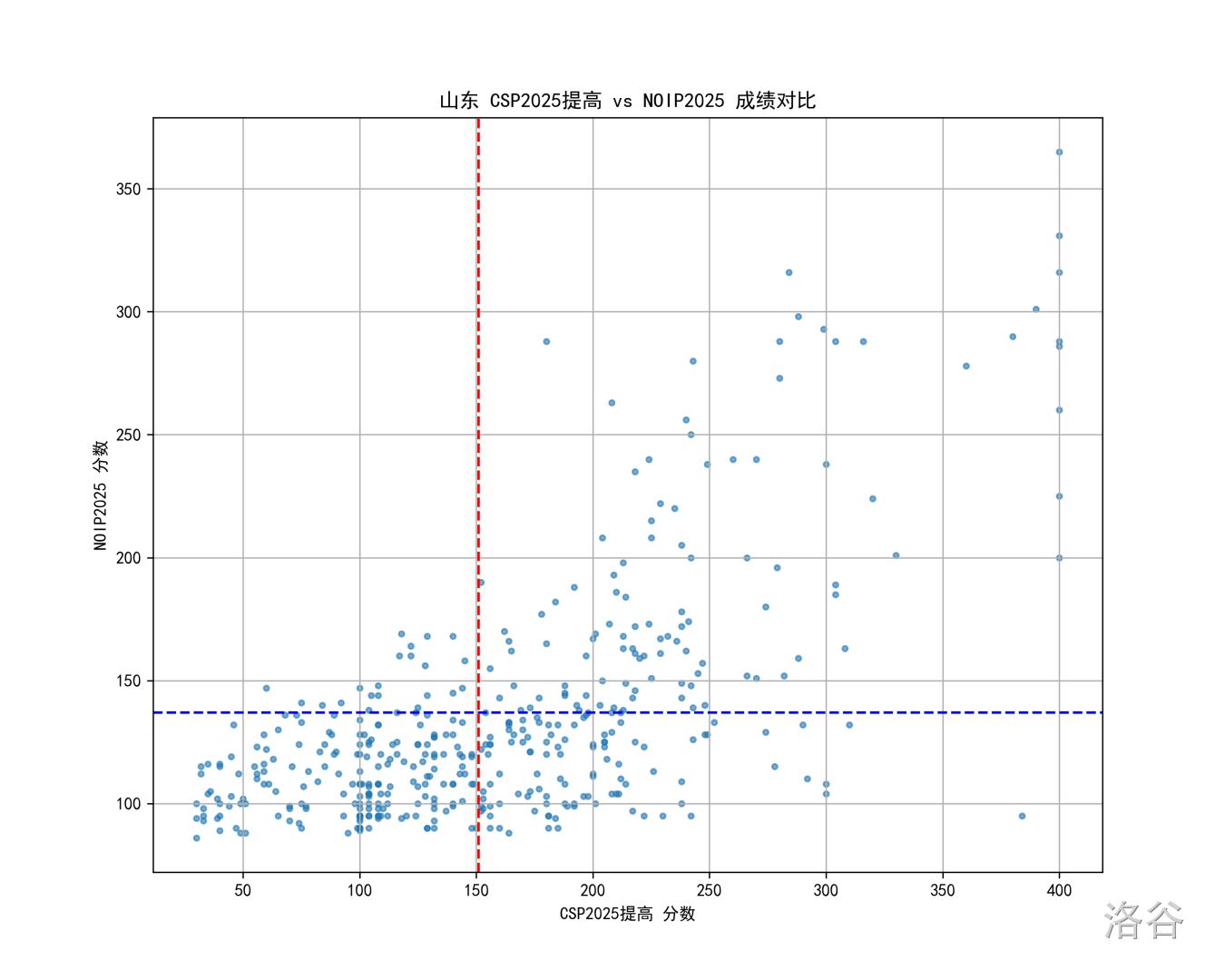
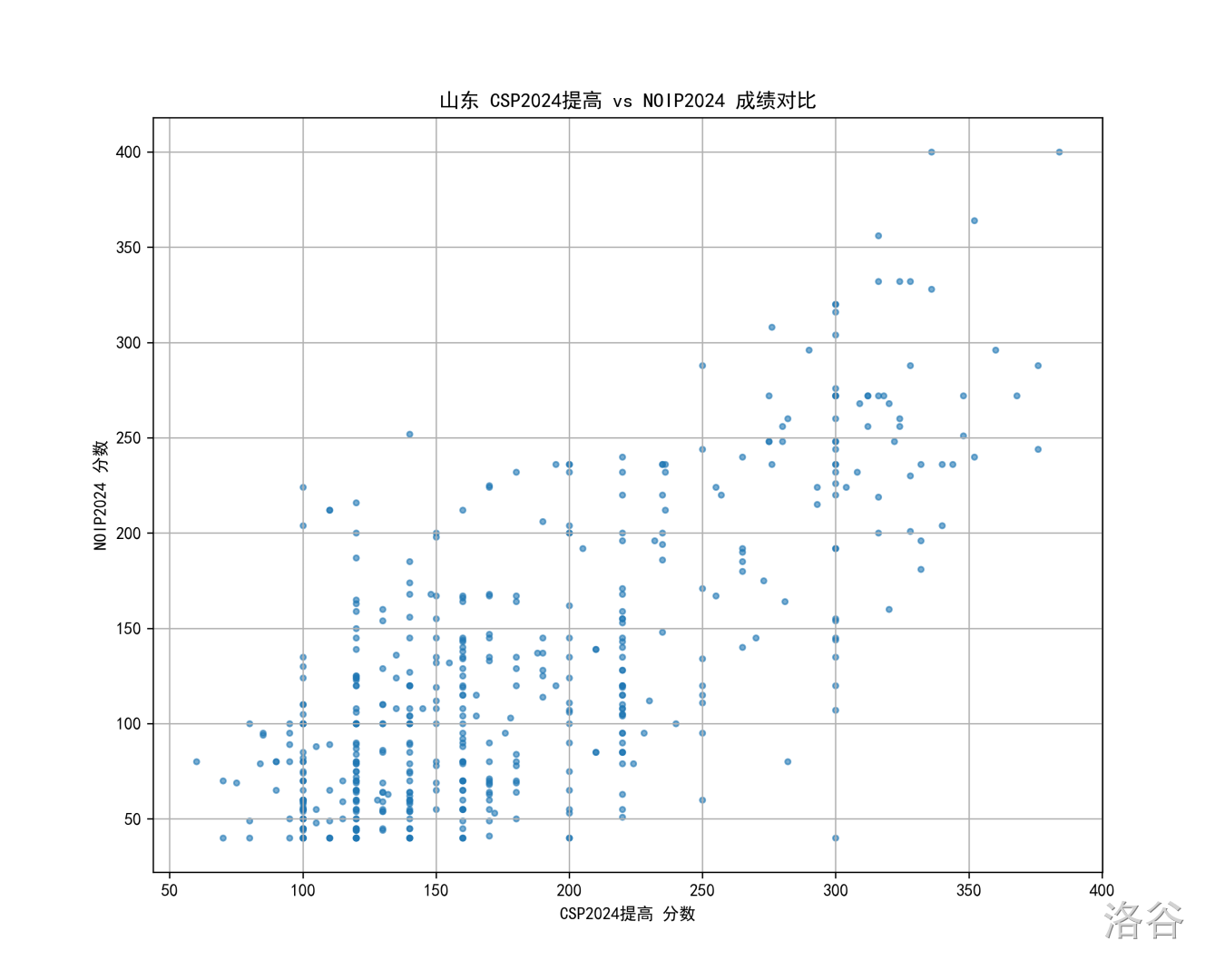
江苏

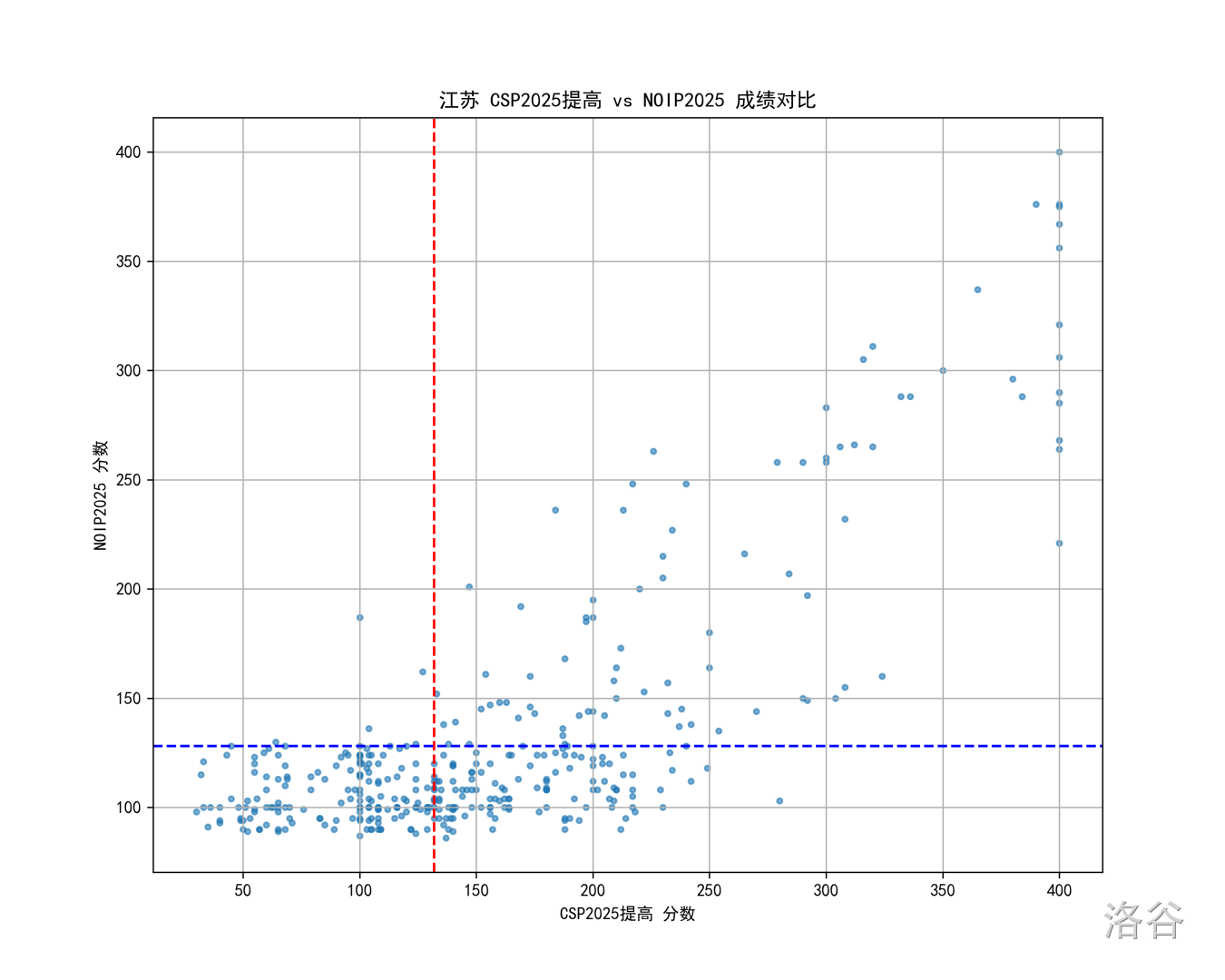
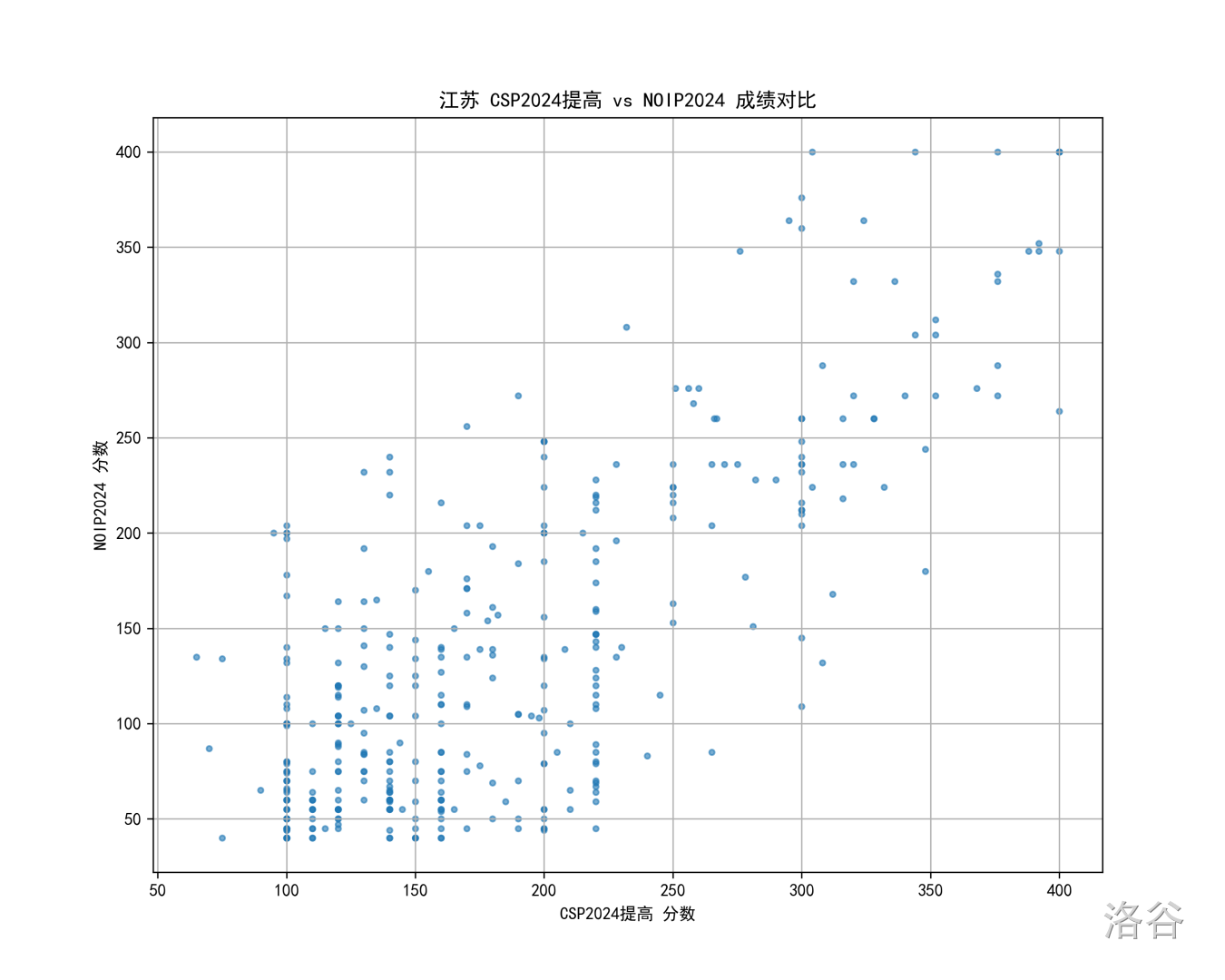
四川

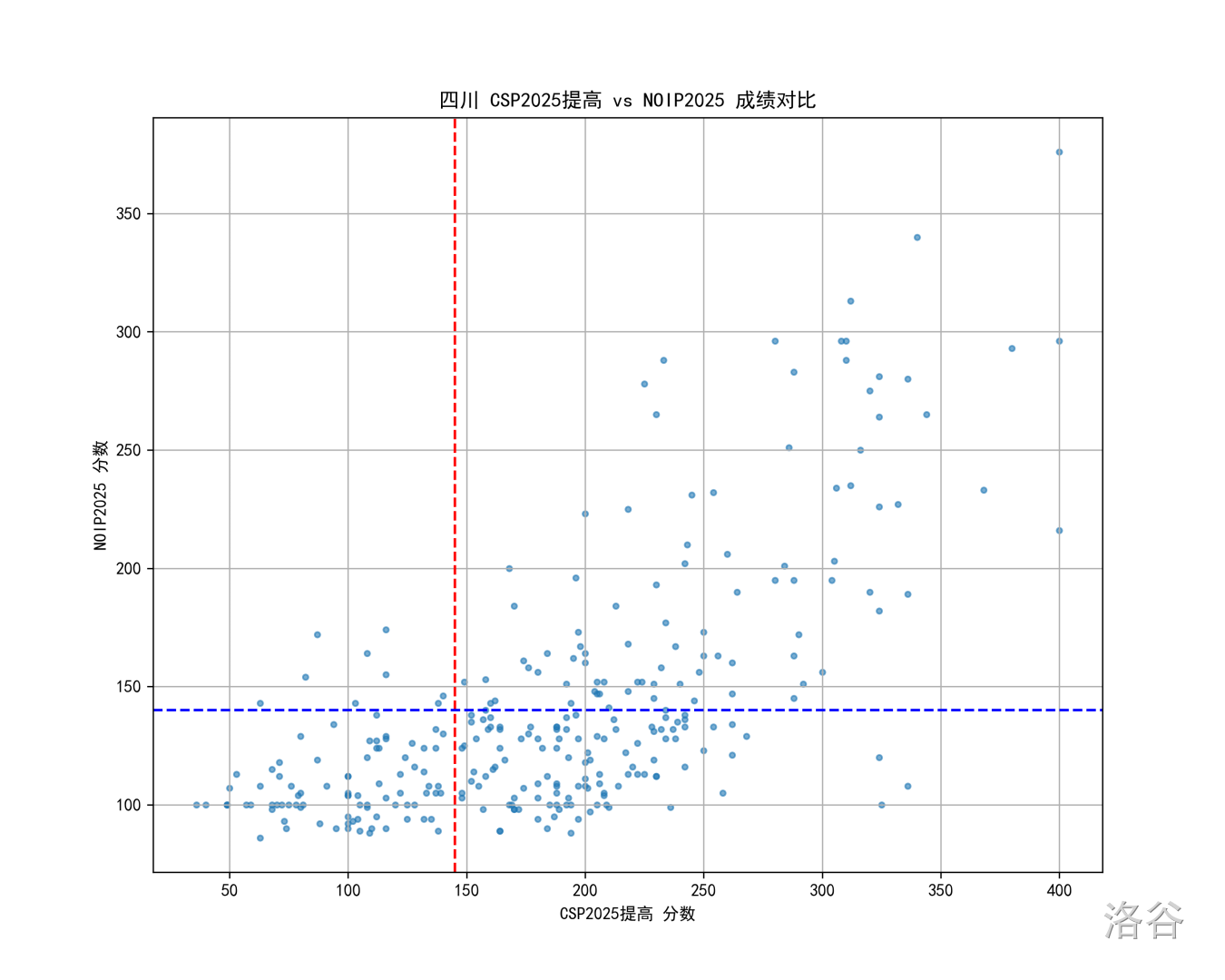
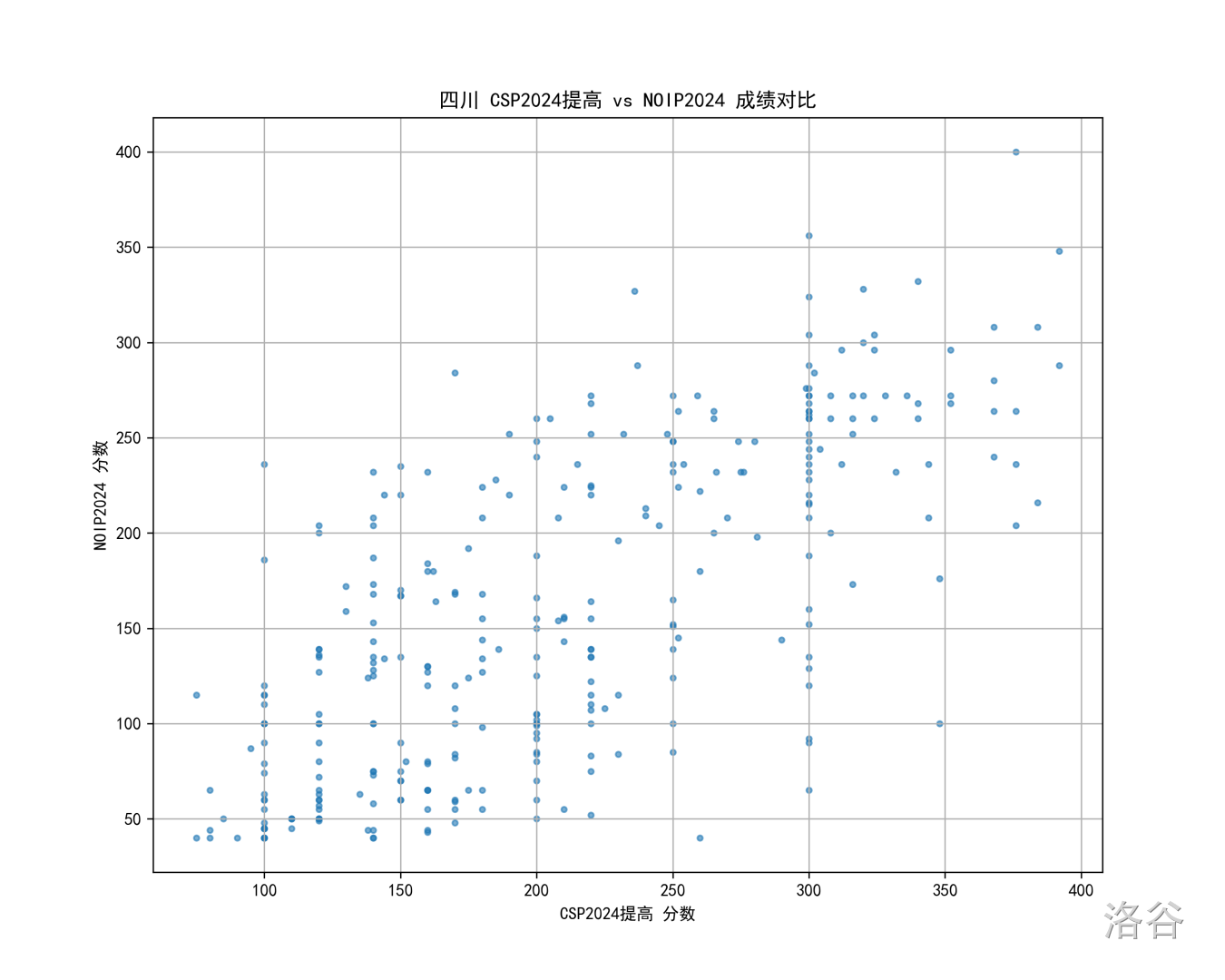
代码

（大部分代码由 GPT5.2 完成）
数据来自于 OIerDB 的 raw.txt，可以在 https://github.com/OIerDb-ng/OIerDb-data-generator/tree/master/data 下载。
给不熟悉 OIerDB 的同学科普下，这个文件很牛，因为它简单粗暴地记录了 OIerDB 的几乎所有信息，而且存储形式是非常粗暴的逗号分隔值（CSV）格式的表格，以当前时刻为例，这个文件里共有 292150 行形如：
CPP
NOIP2025,三等奖,XXX,高一,广州市执信中学,86,广东,男,
NOIP2025,三等奖,XXX,高一,西宁市第二中学,70,青海,男,
NOIP2025,三等奖,XXX,高一,青海湟川中学,70,青海,男,
格式的数据，所以想怎么处理都很方便。
完整代码如下：
PYTHON
import matplotlib.pyplot as plt
from collections import defaultdict
import matplotlib
matplotlib.rcParams['font.family'] = 'SimHei'  # SimHei 是常见的中文字体

import math

def _mean(a: list[float]) -> float:
    return sum(a) / len(a)

def _rankdata(a: list[float]) -> list[float]:
    # average ranks for ties, ranks start at 1
    n = len(a)
    order = sorted(range(n), key=lambda i: a[i])
    ranks = [0.0] * n
    i = 0
    while i < n:
        j = i
        v = a[order[i]]
        while j < n and a[order[j]] == v:
            j += 1
        avg_rank = (i + 1 + j) / 2.0
        for k in range(i, j):
            ranks[order[k]] = avg_rank
        i = j
    return ranks

def _pearsonr(x: list[float], y: list[float]) -> float:
    mx, my = _mean(x), _mean(y)
    num = sum((a - mx) * (b - my) for a, b in zip(x, y))
    denx = math.sqrt(sum((a - mx) ** 2 for a in x))
    deny = math.sqrt(sum((b - my) ** 2 for b in y))
    if denx == 0 or deny == 0:
        return float("nan")
    return num / (denx * deny)


# 计算 rho
def spearman_rho(x: list[float], y: list[float]) -> float:
    rx = _rankdata(x)
    ry = _rankdata(y)
    return _pearsonr(rx, ry) # rho 其实是排名序列的 pearson 相关系数

S1={"重庆":217,"浙江":166,"广东":152,"山东":151,"上海":151,"四川":145,"北京":145,"湖南":140,"江苏":132,"福建":132,"安徽":115} # 25 S 一等线
N1={"重庆":208,"浙江":144,"广东":144,"山东":137,"上海":148,"四川":140,"北京":144,"湖南":149,"江苏":128,"福建":143,"安徽":129} # 25 NOIP 一等线

file_path = 'C:\\xxx\\raw.txt'  # 请替换为你的 raw.txt 路径
contest1 = "CSP2025提高"
contest2 = "NOIP2025"
# contest1 = "CSP2024提高"
# contest2 = "NOIP2024"
# contest1 = "CSP2023提高"
# contest2 = "NOIP2023"
place = "北京"

def read_data(file_path):
    data = defaultdict(dict)
    with open(file_path, 'r', encoding='utf-8') as f:
        for line in f:
            parts = line.strip().split(',')
            if len(parts) < 8:
                continue  # 跳过不完整的数据
            contest, _, name, _, _, score, region, _, _ = parts
            if region != place:
                continue
            try:
                data[name][contest] = float(score)
            except:
                # print("error :", parts)
                pass
    return data

def find_common_participants(data, contest1, contest2):
    common_scores = []
    for name, contests in data.items():
        if contest1 in contests and contest2 in contests:
            # print(name, contests)
            common_scores.append((contests[contest1], contests[contest2]))
    print("同时参加两场比赛的人数：", len(common_scores))
    return common_scores

def plot_scores(common_scores, contest1, contest2):
    if not common_scores:
        print("没有找到同时参加两个比赛的选手。")
        return
    
    print(f"{place} {contest1} {contest2} 斯皮尔曼：", spearman_rho([x[0] for x in common_scores], [x[1] for x in common_scores]))
    x, y = zip(*common_scores)
    plt.figure(figsize=(10, 8))
    plt.scatter(x, y, alpha=0.6, s=10)
    
    if "2025" in contest1:
        plt.axvline(x=S1[place], color='r', linestyle='--')
        plt.axhline(y=N1[place], color='b', linestyle='--')
    plt.xlabel(f'{contest1} 分数')
    plt.ylabel(f'{contest2} 分数')
    plt.title(f'{place} {contest1} vs {contest2} 成绩对比')
    plt.grid(True)
    plt.savefig(f'result_{place}_{contest1}_{contest2}.png', dpi=300)
    plt.show()

def main():
    
    data = read_data(file_path)
    common_scores = find_common_participants(data, contest1, contest2)
    plot_scores(common_scores, contest1, contest2)

if __name__ == "__main__":
    main()
运行时先将 raw.txt 下载到本地，修改 contest1、contest2、place变量的内容即可。（不要吐槽我用这种硬编码的方式写。）不仅局限于 CSP-NOIP 的散点图，这个程序能画的散点图应该还很多。

评论

共 136 条评论，欢迎与作者交流。

正在加载评论...