专栏文章
2024 年高考数学·新课标 I 卷 T11/T18/T19
学习·文化课参与者 1已保存评论 2
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 2 条
- 当前快照
- 1 份
- 快照标识符
- @minklht8
- 此快照首次捕获于
- 2025/12/02 03:56 3 个月前
- 此快照最后确认于
- 2025/12/02 03:56 3 个月前
2024 年高考数学·新课标 I 卷
T11
题面
造型 可以看作途中曲线 的一部分,已知 过坐标原点 ,且 上的点满足横坐标大于 ,到点 的距离与到定直线 的距离之积为 ,则 ________。
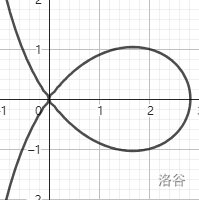
- 点 在 上
- 在第一象限的点的纵坐标的最大值为
- 当点 在 上时,
题解
正确答案:
- 选项分析
在曲线 上
到 的距离为
- 选项分析
由上述分析易知
将 代入得原方程成立
点 在 上
- 选项分析
在 左侧存在 满足
在第一象限的点的纵坐标的最大值大于
- 选项分析
当点 在 上时,
T18
题面
已知函数
- 若 ,且 ,求 的最小值。
- 证明:曲线 是中心对称图形。
- 若 当且仅当 ,求 的取值范围。
题解
当 时,
即
当 时,
是关于 的中心对称图形
由题,
假设 ,由
应用零点存在定理知存在
该结论与 矛盾
此时,
当 时, 且不恒为
在 递增,其中,当且仅当 时,
当 时,令
且当 时,
在 递减
而 ,此时矛盾
综上所述,
T19
题面
设 为正整数,数列 是公差不为 的等差数列,若从中删去两项 和 后剩余的 项都可被平均分为 组,且每组的 个数都能构成等差数列,则称数列 是 。
- 写出所有的 ,使数列 是 。
- 当 时,证明:数列 是 。
- 从 中一次任取两个数 和 ,记数列 是 的概率为 ,证明:。
题解
由题,显然有
去掉 后剩下
该 个可分割为以下三个四元组
当 中 时,连续四个分为一组即可
数列 是
实则是不会写了,嘴硬说是不想写 了。
相关推荐
评论
共 2 条评论,欢迎与作者交流。
正在加载评论...