题解：P12537 [XJTUPC 2025] 罗斯飞鸽

出题人题解。

这个题出的时候没想过还能三维偏序。我们先考察

v = 1

的情况：将判定点画在

xOt

平面上，从某个判定点出发，能到达的点的范围在它的左上 45 度到右上 45 度之间。

如下：

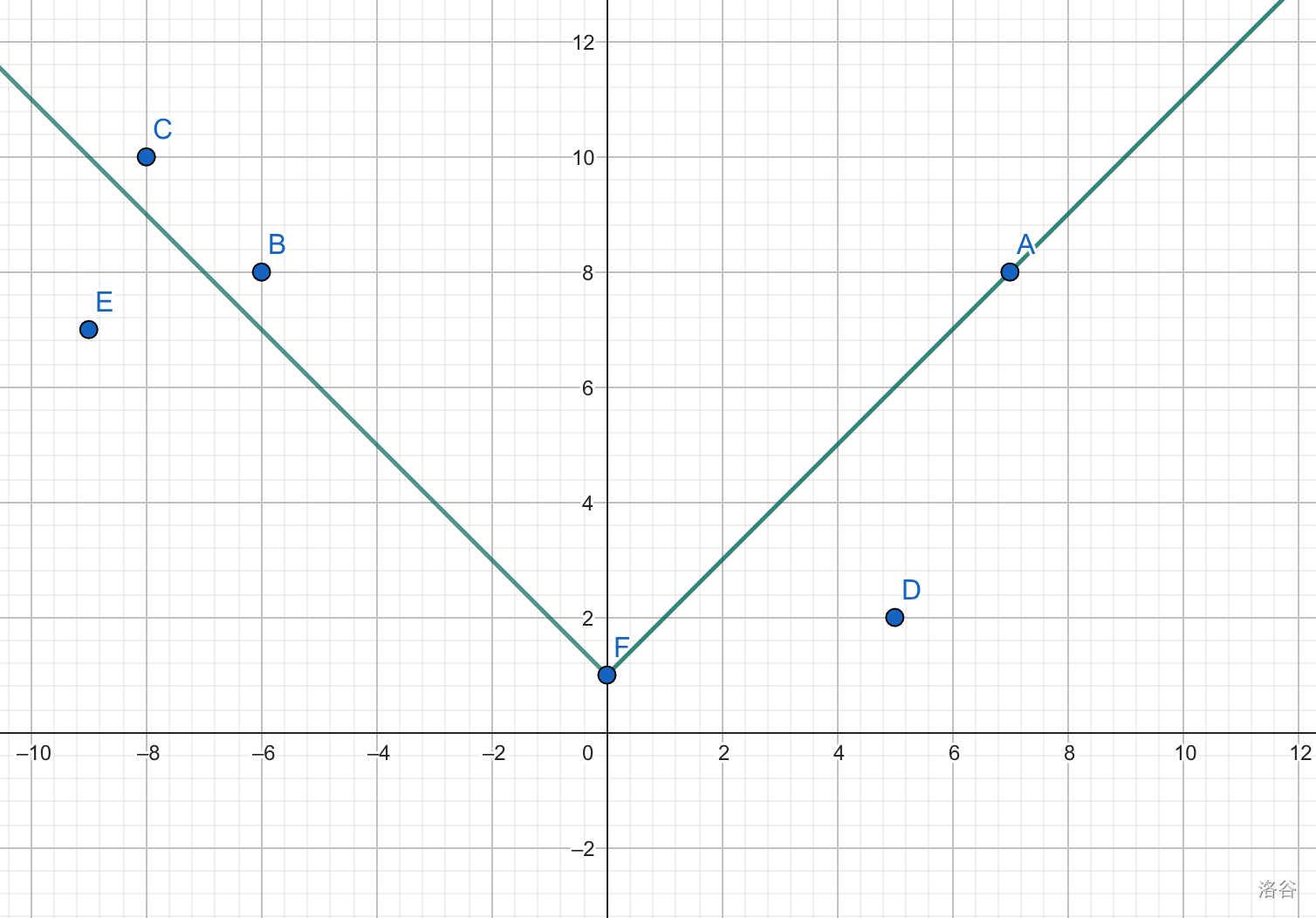
这是第一组样例对应的情况，如果判定了 F 点，下一步可判定的就是 A,B,C 之一。

这个画图似乎对解题没有帮助？并不！我们把整个图片旋转 45 度：

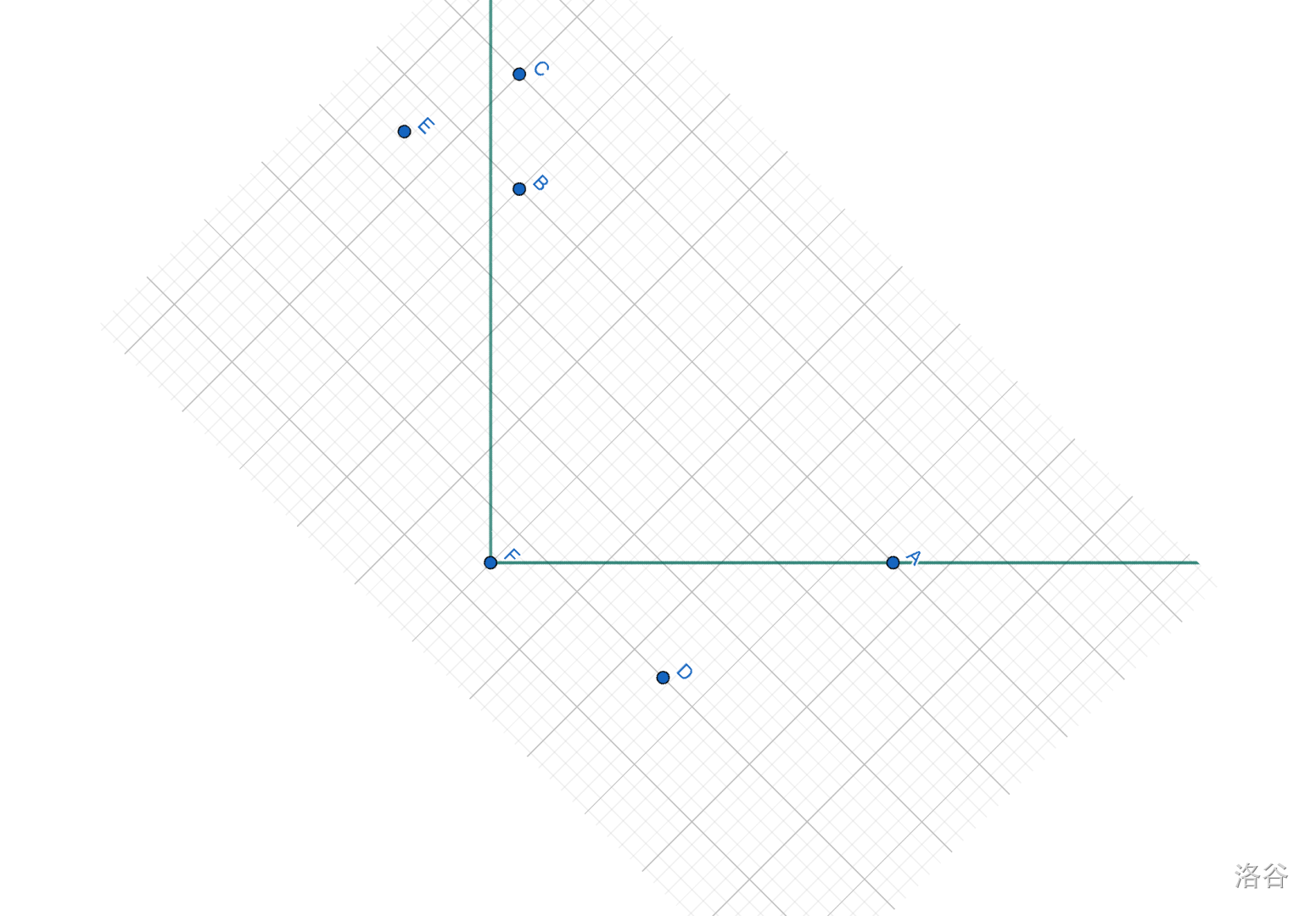
所以，此时每个点能到达的下一个点，就是位于右上方的点。这是一个“二维偏序最长链问题”，如果将所有点按照新的横坐标排序，就是在求新的纵坐标的最长不下降子序列。

形式化地，新的坐标是

(t + x, t - x)

。

不过，完整的题目要考虑

v

。所以实际上，一个点能到达的点是一个

\pm \arctan(v)

的角度范围。以

v=2

为例：

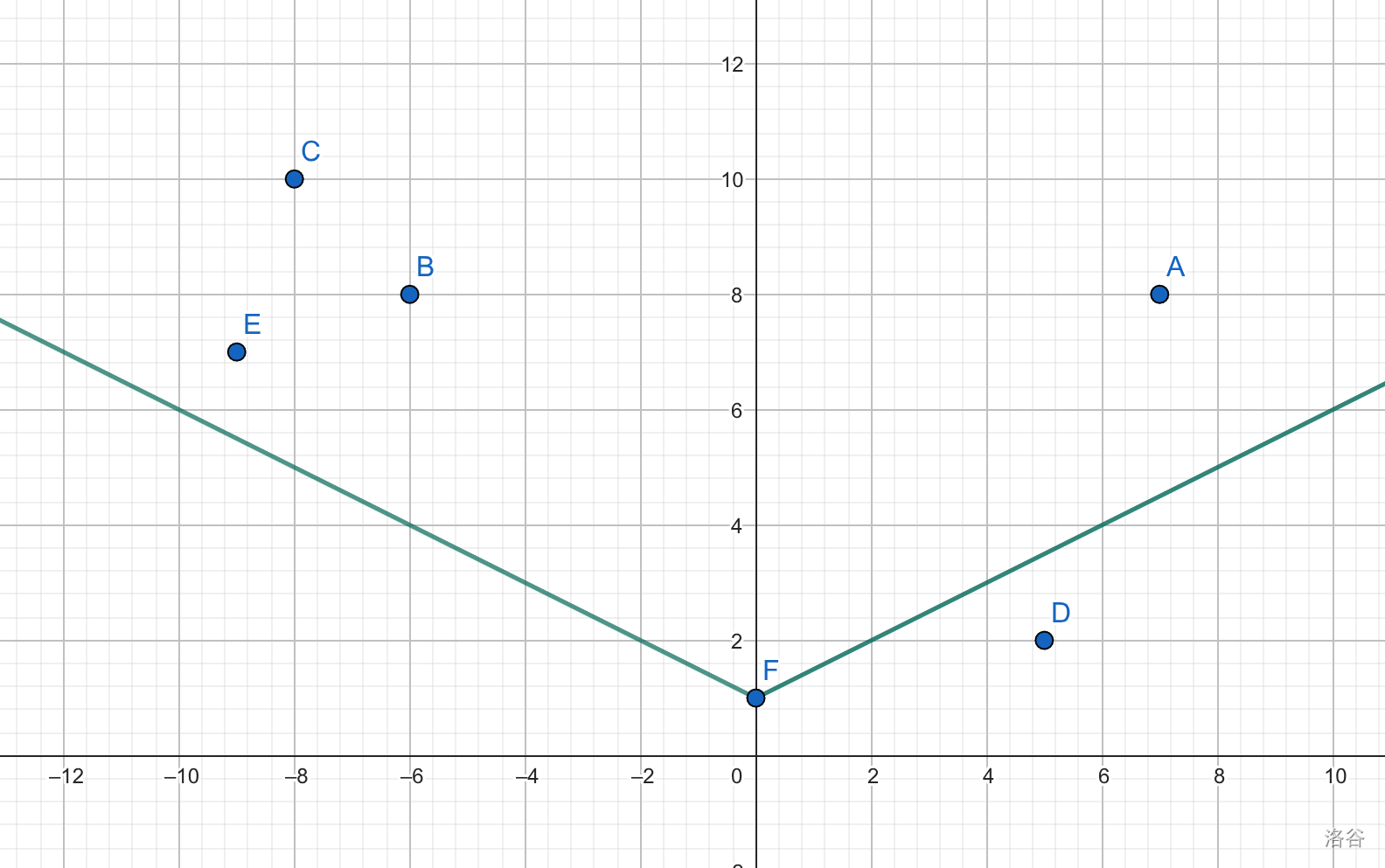
此时，我们在进行旋转运算的同时，还要向 t 轴方向做一个伸缩变换。感性理解，这两个变换显然不会改变可达点集。

形式话地说，得到的新坐标是

(vt+x, vt-x)

，然后跑最长不下降子序列就好了。

题解 pdf 里那个证明更严谨一点。

代码：

CPP

#include <bits/stdc++.h>
using namespace std;
 
const int MAXN(5e5 + 5);
 
struct Node {
    long long ta, tb;
};
 
int n;
long long v;
Node a[MAXN], len[MAXN];
 
bool operator<(Node x, Node y) {
    return x.ta != y.ta ? x.ta < y.ta : x.tb < y.tb;
}
 
bool compare(Node x, Node y) {
    return x.tb != y.tb ? x.tb < y.tb : x.ta < y.ta;
}
 
void solve() {
    scanf("%d %lld", &n, &v);
    for (int i = 1; i <= n; i++) {
        long long t, x;
        scanf("%lld %lld", &t, &x);
        a[i].ta = v * t + x;
        a[i].tb = v * t - x;
    }
    sort(a + 1, a + n + 1, compare);
    int ans = 0;
    len[0].ta = len[0].tb = LLONG_MIN;
    for (int i = 1; i <= n; i++) {
        int p = lower_bound(len, len + ans + 1, a[i]) - len;
        len[p] = a[i];
        if (p > ans) ans++;
    }
    printf("%d\n", ans);
}
 
int main() {
    int _;
    scanf("%d", &_);
    while (_--) {
        solve();
    }
    return 0;
}

题解：P12537 [XJTUPC 2025] 罗斯飞鸽

文章操作

相关推荐

评论

题解：P12537 [XJTUPC 2025] 罗斯飞鸽