专栏文章

题解：P3796 AC 自动机（简单版 II）

CCosmos_zzx
P3796题解参与者 3已保存评论 3

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
3 条
当前快照
1 份
快照标识符
@minbxxjj
此快照首次捕获于
2025/12/01 23:54
3 个月前
此快照最后确认于
2025/12/01 23:54
3 个月前
查看原文
依旧模板题。
建议先过【模板】AC 自动机。
不懂什么是AC自动机的可以看ACAM 学习笔记 | 附 YbtOJ 全部题解 。
这里重点讲一下如何拓扑优化（当然不拓扑优化也能过）。

拓扑优化ACAM

原来暴力跳 failfail 指针的时间复杂度是趋近于 O(S1×S2)O(S_1\times S_2) 的，其中 S1S_1 是模式串总长，S2S_2 是文本串总长。
如何优化成 O(S2)O(S_2)？
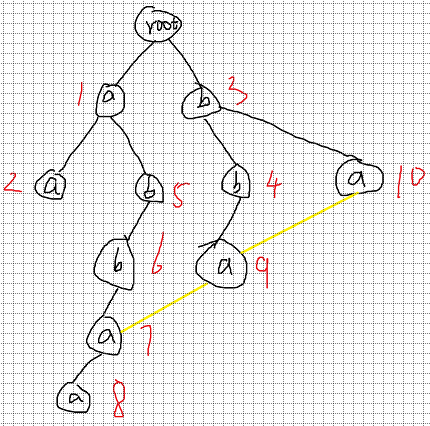
我们可以发现编号 77 的 failfail 是 99，99 的 failfail 是 1010，那么在更新的时候 7→9→107\rightarrow 9 \rightarrow 10 分别都更新了一次，但是在更新 9→109\rightarrow 10 的时候又更新了一遍，我们能否将每个点只更新一遍达到所需效果？
答案是可以的。我们先让每个点存储自己的信息，再通过拓扑排序将这些信息从深度较深的点传到深度较浅的点，为什么可以这么做？因为拓扑排序可以从入度为 00 的点开始，而我们的图去掉原来的边再加上 failfail 所指的有向边正是一个DAG，且深度较深的点正好就是入读为 00 的点，所以我们可以用拓扑排序解决问题。
CPP
#include<bits/stdc++.h>
#define int long long
typedef long long ll;
using namespace std;
const int N=2e5+114;
int n,cnt,in[N];
string ss[N];
struct Tire
{
    int nxt;
    int s[27];
    int ed;
    int sum;
}tr[N];
void Tire_build(string s)
{
    int now=0;
    for(int i=0;i<s.size();i++)
    {
        if(!tr[now].s[s[i]-'a'])tr[now].s[s[i]-'a']=++cnt;
        now=tr[now].s[s[i]-'a'];
    }
    tr[now].ed++;
}
void Get_Fail()
{
    queue<int> q;
    for(int i=0;i<26;i++)if(tr[0].s[i])q.push(tr[0].s[i]);
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        for(int i=0;i<26;i++)
        {
            if(!tr[t].s[i])tr[t].s[i]=tr[tr[t].nxt].s[i];
            else tr[tr[t].s[i]].nxt=tr[tr[t].nxt].s[i],q.push(tr[t].s[i]),++in[tr[tr[t].s[i]].nxt];
        }
    }
}
void topu()
{
    queue<int> q;
    for(int i=1;i<=cnt;i++)if(!in[i])q.push(i);
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        int t2=tr[t].nxt;
        tr[t2].sum+=tr[t].sum;
        --in[t2];
        if(!in[t2])q.push(t2);
    }
}
void find(string s)
{
    int now=0;
    for(int i=0;i<s.size();i++)
    {
        now=tr[now].s[s[i]-'a'];
        tr[now].sum++;
    }
}
int find_mo(string s)
{
    int now=0;
    for(int i=0;i<s.size();i++)
    {
        now=tr[now].s[s[i]-'a'];
    }
    return tr[now].sum;
}
signed main()
{
    while(cin>>n && n!=0)
    {
        memset(tr,0,sizeof tr);
        cnt=0,memset(in,0,sizeof in);
        for(int i=1;i<=n;i++)
        {
            cin>>ss[i];
            Tire_build(ss[i]);
        }
        Get_Fail();
        string s;
        cin>>s;
        find(s);
        topu();
        int maxn=0;
        for(int i=1;i<=n;i++)
            maxn=max(maxn,find_mo(ss[i]));
        cout<<maxn<<endl;
        for(int i=1;i<=n;i++)if(find_mo(ss[i])==maxn)cout<<ss[i]<<endl;
    }
    return 0;
}

评论

共 3 条评论，欢迎与作者交流。

正在加载评论...