专栏文章

巴什博弈 与 威佐夫博弈 与 动态 k 倍减法

___staring__
算法·理论参与者 5已保存评论 5

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
5 条
当前快照
1 份
快照标识符
@miqrow3x
此快照首次捕获于
2025/12/04 09:38
3 个月前
此快照最后确认于
2025/12/04 09:38
3 个月前
查看原文
若以下内容出现了谬误，烦请私信我进行指正，以及可私信提问。

问题一 (巴什博弈)

有一堆石子，石子数为 nn ，先手 A 和后手 B 轮流取，每次取 [1,k][1,k] 内的整数个石子，无法操作的人判负，问什么情况下先手必胜，或先手必败。
显然我们知道答案为，当且仅当 (k+1)∤n(k+1) \nmid n 先手必胜，否则先手必败。
这是因为我们遇见过这道题，但假使我们没见过，我们也可以从头推出这个结论。
记 f(n)f(n) 表示 nn 个石子时胜负情况，即 f(n)=1f(n)=1 代表先手必胜，f(n)=0f(n)=0 代表先手必败。
显然 f(0)=0f(0)=0 ，这是游戏的边界情况。
f(1)=1f(1)=1 ，这是因为先手可以一步拿走唯一的石子。
f(2)=1f(2)=1 ，当先手取一个石子时必败，取两个石子时必胜，显然先手应该取两个石子。
f(3)=1f(3)=1 ，同上，先手应该取三个石子。
可以发现，当 n∈[1,k]n \in [1,k] 时，先手总是可以一次取完，即 f(n)=1f(n)=1 均成立。
而当 n=k+1n=k+1 时，先手无法再一步取完，此时局面变成后手操作，剩下的石子数 n′=n−x∈[1,k]n'=n-x \in [1,k] ，而我们有 f(n′)=1f(n')=1 ，因此后手必胜，即先手必败。
当 n∈[k+2,2k+1]n \in [k+2,2k+1] 时，先手又可以一步取走 n mod (k+1)n \bmod (k+1)，使得 n′=k+1n'=k+1 ，把必败态转到后手，自己必胜。
那么同上可知，f(n)=1f(n)=1 当且仅当 ∃i∈[1,k],f(n−i)=0\exist i \in [1,k],f(n-i)=0 ，或者 f(n)=0f(n)=0 当且仅当 ∀i∈[1,k],f(n−i)=1\forall i \in [1,k],f(n-i)=1 ，以及边界情况 f(0)=0f(0)=0。
那么我们就能推出 f(n)=0⇔(k+1)∣nf(n)=0 \Leftrightarrow (k+1) \mid n。
同时，先手的策略应是每次取走 nmod  (k+1)n \mod (k+1) 个石子。

问题二 (威佐夫博弈)

有两堆石子，石子数为 a,ba,b ，先手 A 和后手 B 轮流取，每次可以单独取一堆中的任意石子数，或是两堆同时取相同石子数，无法操作的人判负，问什么情况下先手必胜，或先手必败。
根据问题一的推导过程，我们可以记 f(a,b)f(a,b) 表示先手的胜负情况，边界为 f(0,0)=0f(0,0)=0。
同时根据问题一的结论，我们有 f(a,b)=1f(a,b)=1 当且仅当，∃x≤a,f(a−x,b)=0\exist x \leq a,f(a-x,b)=0 或 ∃x≤b,f(a,b=x)=0\exist x \leq b,f(a,b=x)=0 或 ∃x≤min⁡(a,b),f(a−x,b−x)=0\exist x \leq \min(a,b),f(a-x,b-x)=0。
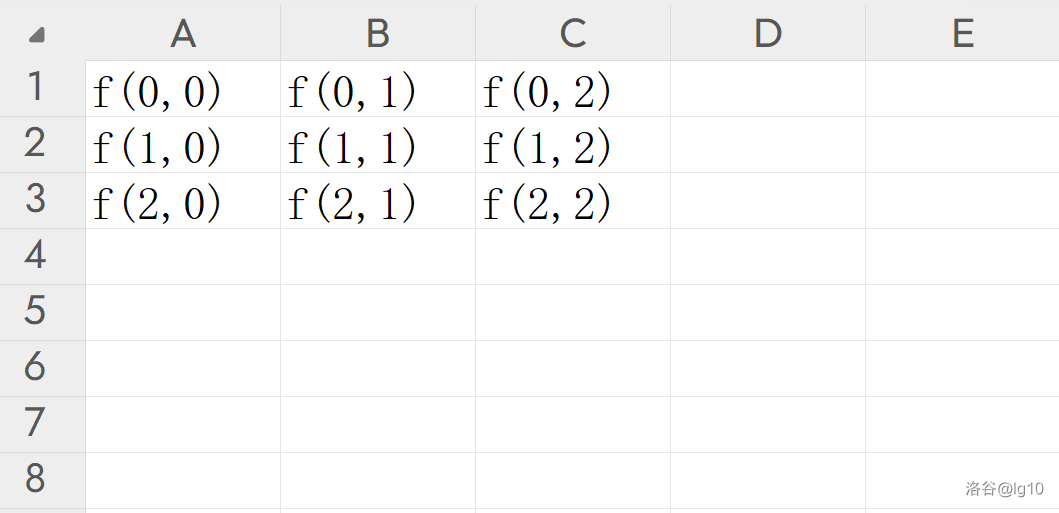
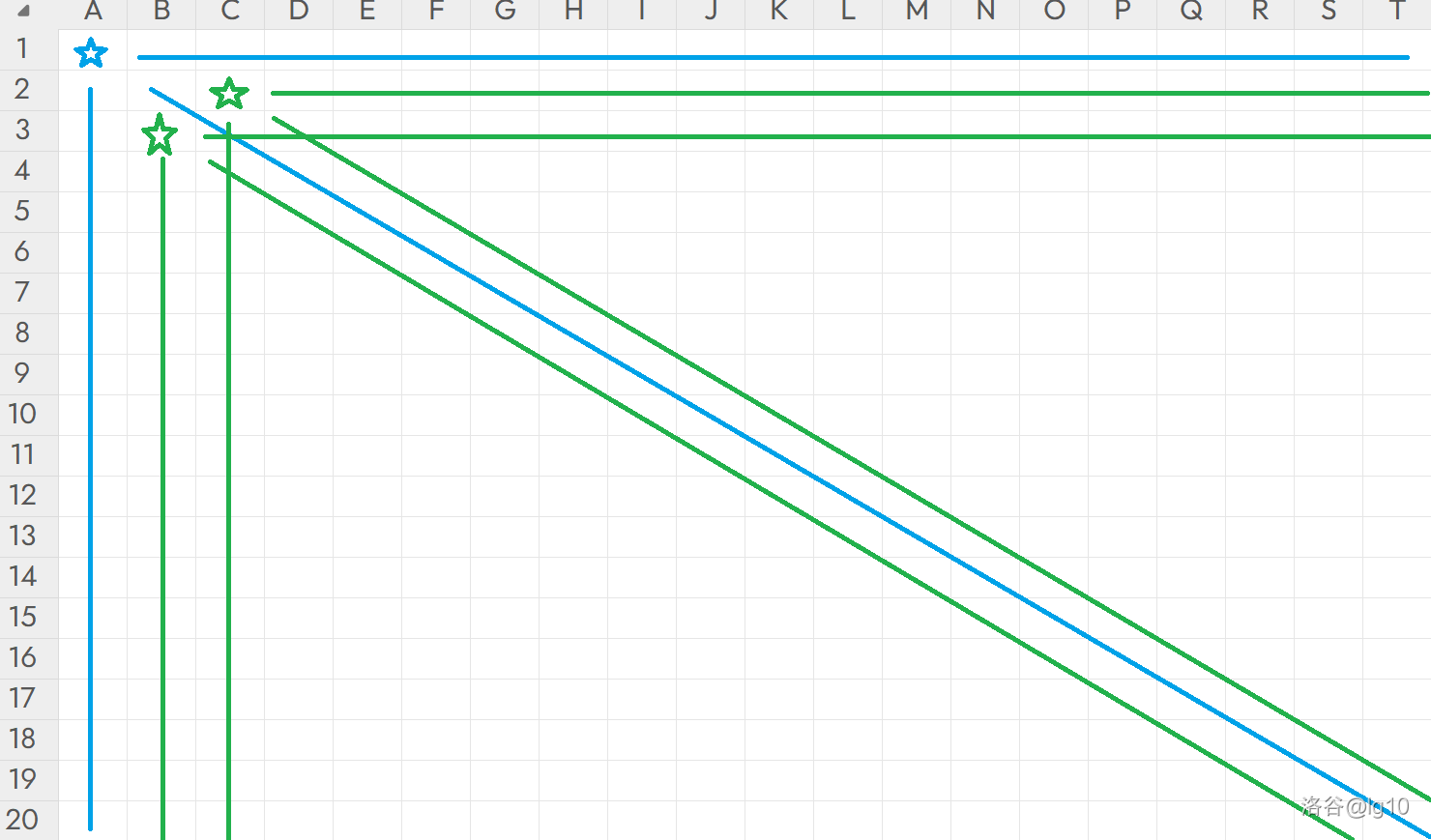
写出式子似乎不太好观察，那我们把 ff 搬到平面上，第 aa 行 bb 列的元素代表 f(a,b)f(a,b) 的值，比如下面的 excel。
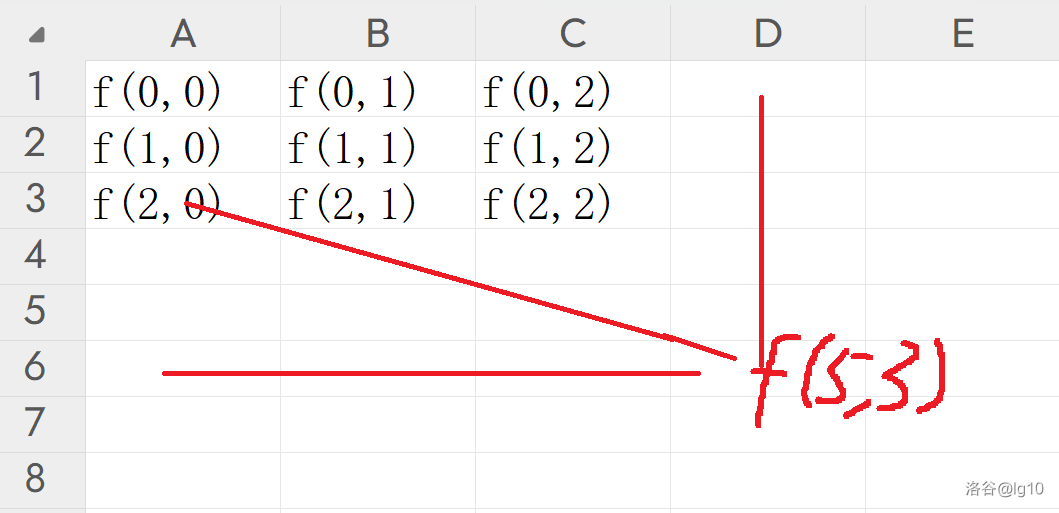
那么 f(a0,b0)f(a_0,b_0) 的前驱，即计算 f(a0,b0)f(a_0,b_0) 的值需要的点，应该在这样的红线上：
只要这三条线上出现了 =0=0 的点，f(a,b)=1f(a,b)=1。
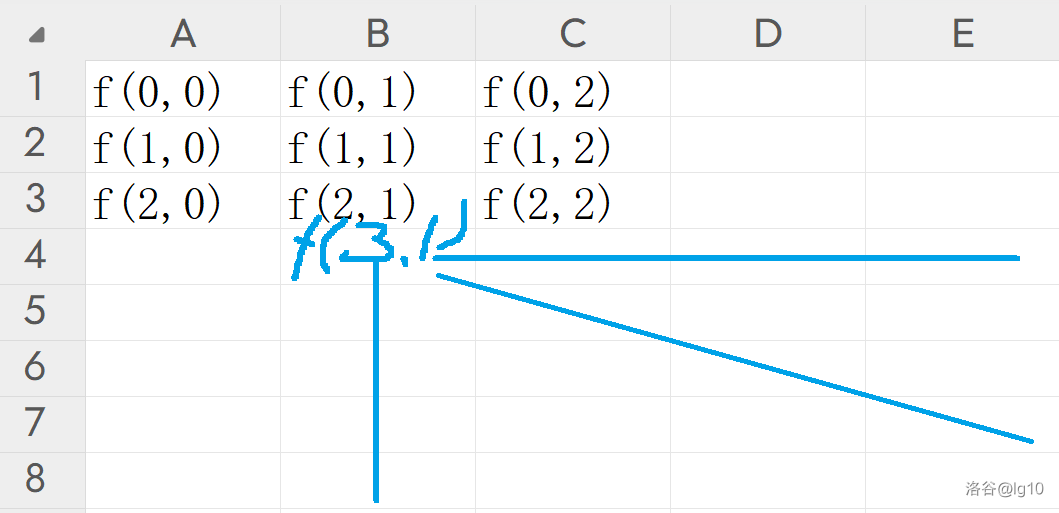
似乎还是不好计算，那么我们正难则反，考虑一个 f(a,b)=0f(a,b)=0 的点会使哪些点 =1=1。
即蓝线上的点一定 =1=1 ，如上图中若 f(3,1)=0f(3,1)=0 则 f(5,3)=1f(5,3)=1。
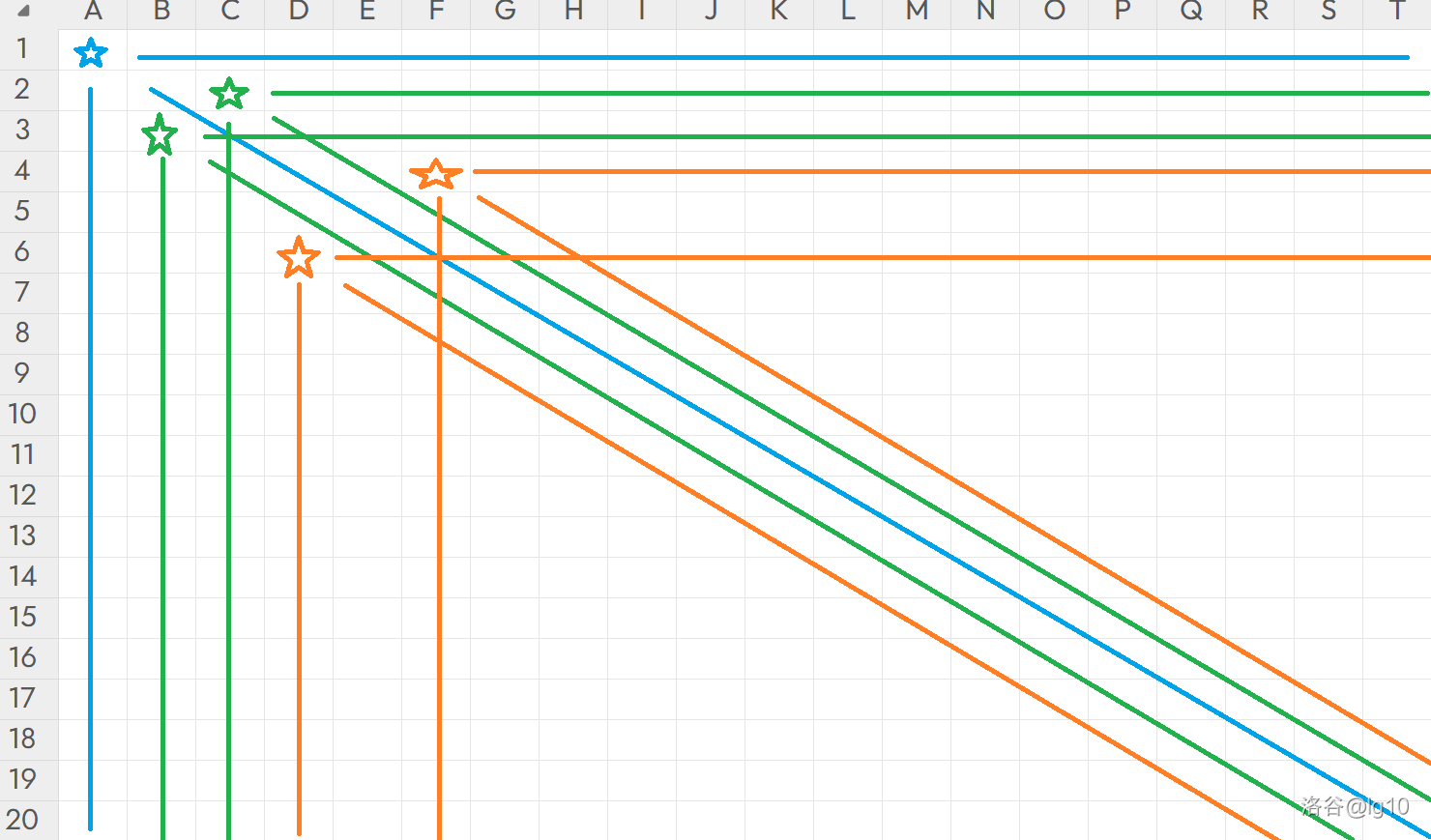
那么现在的情况似乎就简单一些了，我们从边界 f(0,0)=0f(0,0)=0 开始，把蓝线上的点删掉，并将当前一定不会再被删掉点加入。
即初始：
接下来把 f(1,2)f(1,2) 和 f(2,1)f(2,1) 覆盖：
之后是 f(3,5)f(3,5) 和 f(5,3)f(5,3)：
以此类推。
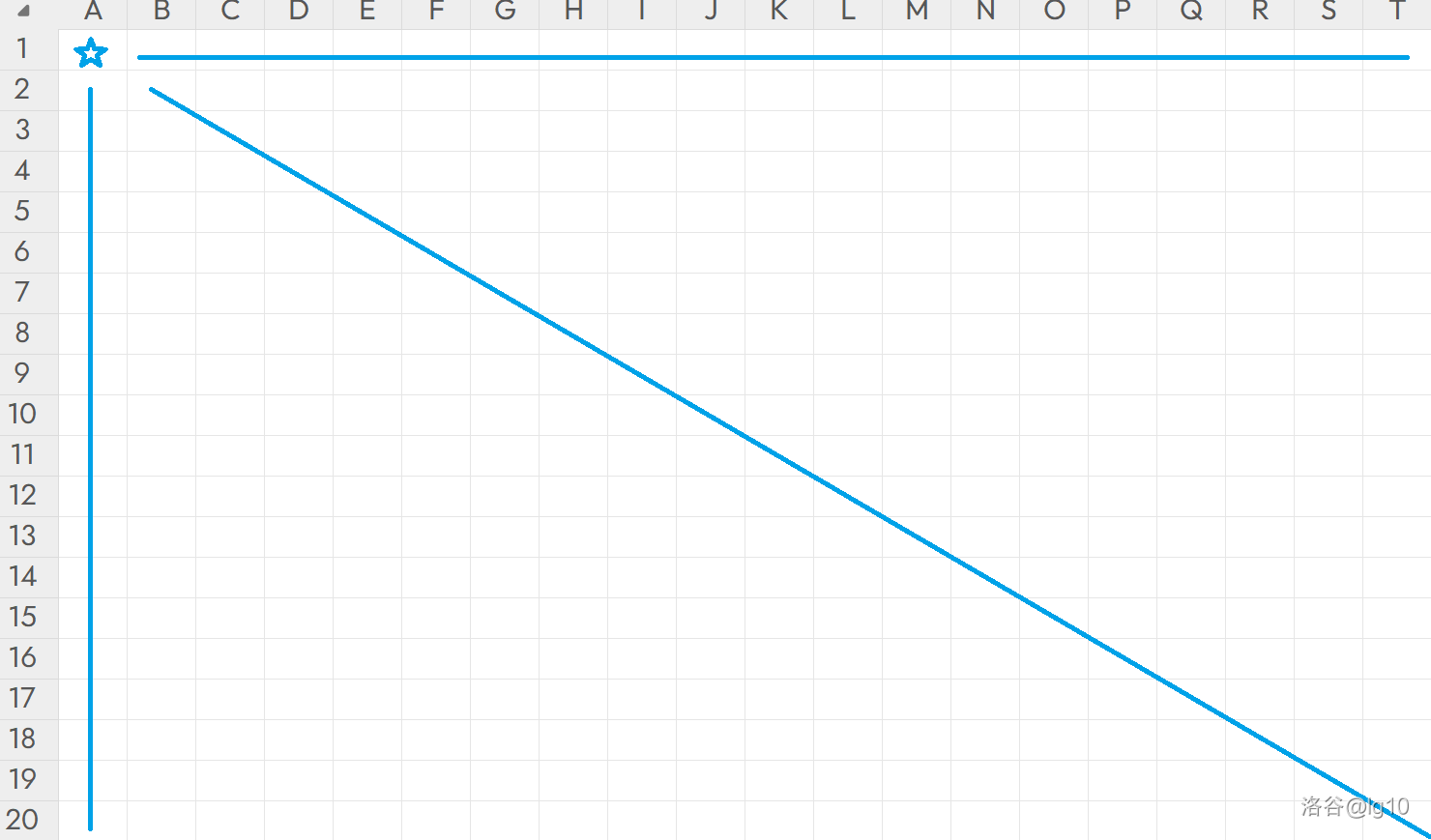
显然地，我们发现，每行每列只会有一个星，并且整个平面呈轴对称，那我们只考虑这些星星的一半，即 f(a,b)=0,a<bf(a,b)=0,a<b 的点。
根据图片且自己推导可以得到前几个点是 (0,0),(1,2),(3,5),(4,7),(6,10),(8,13)(0,0),(1,2),(3,5),(4,7),(6,10),(8,13)。
发现似乎有些规律，其中可以看图且比较易证的有：aia_i 递增，bib_i 递增，bi−ai=ib_i-a_i=i，i≤ai≤2ii \le a_i \le 2i。
以及实际上，我们有 ai=mex⁡(⋃j=1i−1{aj,bj})a_i = \operatorname{mex} ( \bigcup_{j=1}^{i-1} \{a_j,b_j\}) ，这也是易证的。
那么我们已经可以递推出所有项了，但我们还可以继续探究增长率。
对于第 kk 行，由于 k≤ak≤2kk \le a_k \le 2k ，那么当 k→∞k \rightarrow \infty 时，aka_k 与 kk 应该呈正比例，那么我们设 ak=ϕka_k=\phi k。
同时因为 bib_i 递增，总存在一个最大的 tt 使得 bt<akb_t<a_k 且 bt+1>akb_{t+1}>a_k ，同时此时 bt∼akb_t \sim a_k。
那么，我们有 ak=ϕk=k+t,ϕt+t=bt=ϕka_k=\phi k=k+t,\phi t+t=b_t=\phi k ，可以得到 ϕ2−ϕ−1=0\phi^2-\phi-1=0 ，由于 ϕ>0\phi >0 ，显然我们应取 ϕ=1+52\phi = \frac {1+\sqrt5} {2}。
这是个无理数，但我们的点集为整数，那么肯定差了一部分，显然应该不是常数，那么我们猜测是取整函数。
具体来说，由于 ϕ>1\phi>1 ，那么我们有 ⌊ϕk⌋\lfloor \phi k \rfloor 互不相同，而上取整和四舍五入由于 ϕ\phi 是无理数本质相同，所以应该有 ak=⌊ϕk⌋a_k=\lfloor \phi k \rfloor。
那么我们也就有 bk=⌊(ϕ+1)k⌋b_k=\lfloor (\phi+1)k \rfloor，显然这样生成的 {a},{b}\{a\},\{b\} 内部互不相同，但一定满足 {a}∩{b}=∅,{a}∪{b}=N+\{a\} \cap \{b\} = \varnothing,\{a\} \cup \{b\}=\N^+ 吗？（以下证明不考虑 k=0k=0 的特例）。
在证明之前，我们需要知道 1ϕ+1ϕ+1=1\frac {1} {\phi} + \frac {1} {\phi + 1} = 1 ，这是显然的，读者可自行验证。

1. {a}∩{b}=∅\{a\} \cap \{b\} = \varnothing

考虑反证，设正整数 xx 满足 x∈{a}x \in \{a\} 且 x∈{b}x \in \{b\} ，那么一定存在正整数 m,nm,n 满足 x<mϕ<x+1,x<n(ϕ+1)<x+1x < m\phi < x+1,x < n(\phi+1) < x+1。
即 xϕ<m<x+1ϕ,xϕ+1<n<x+1ϕ+1\frac{x}{\phi}<m<\frac{x+1}{\phi},\frac{x}{\phi+1}<n<\frac{x+1}{\phi+1}。
由于 1ϕ+1ϕ+1=1\frac {1} {\phi} + \frac {1} {\phi + 1} = 1，两式相加我们得到 x<m+n<x+1x < m + n < x + 1 ，然而 x,m,nx,m,n 都是正整数，所以一定不存在这样的 xx。

2. {a}∪{b}=N+\{a\} \cup \{b\} = \N^+

同样考虑反证，设正整数 xx 满足 x∉{a}x \notin \{a\} 且 x∉{b}x \notin \{b\} ，那么一定存在正整数 m,nm,n 满足 ⌊mϕ⌋<x<⌊(m+1)ϕ⌋,⌊n(ϕ+1)⌋<x<⌊(n+1)(ϕ+1)⌋\lfloor m\phi \rfloor < x < \lfloor (m+1)\phi \rfloor,\lfloor n(\phi+1) \rfloor < x < \lfloor (n+1)(\phi+1) \rfloor。
由于 ϕ\phi 是无理数，所以有 mϕ<x<(m+1)ϕ−1m\phi < x < (m+1)\phi - 1 ，即 m<xϕ<m+1−1ϕm < \frac{x}{\phi} < m+1-\frac{1}{\phi}。
同理有 n<xϕ+1<n+1−1ϕ+1n < \frac{x}{\phi+1} < n+1-\frac{1}{\phi+1} ，两式相加得到 m+n<x<m+n+1m+n < x < m+n+1 ，同样由于 x,m,nx,m,n 都是正整数，所以不存在 xx。
实际上以上证明来自贝蒂定理。
至此我们证明了，记 ϕ=1+52\phi = \frac{1+\sqrt5}{2} ，得到数列 ai=⌊iϕ⌋,bi=⌊i(ϕ+1)⌋a_i = \lfloor i\phi \rfloor,b_i = \lfloor i(\phi+1) \rfloor ，对于任意 x,yx,y ，f(x,y)=0f(x,y)=0 当且仅当 ∃k,ak=x\exist k,a_k=x 且 bk=yb_k=y。
也即 f(x,y)=0⇔⌊∣y−x∣ϕ⌋=xf(x,y)=0 \Leftrightarrow \lfloor |y-x|\phi \rfloor = x。
此时先手的操作策略为，每次在平面上将当前点移动到任意一个星处即可。

问题三 (动态 k 倍减法)

有一堆石子，石子数为 nn ，先手 A 和后手 B 轮流取，第一次只能取 [1,n−1][1,n-1] 内的整数个石子，之后每个人取的石子数不超过上一个人的 kk 倍，无法操作的人判负，问先手第一次应至少取多少石子才能保证必胜，或先手必败。
注意，kk 可取小数。
（由于 k<1k<1 的情况较为复杂，这里我们只讨论 k≥1k \ge 1 的情况）。

1. k=1k=1

显然我们应从最简单的版本开始讨论。
类似地，我们记 f(n)f(n) 表示先手在 nn 个石子时至少取多少个才能必胜，定义当 f(n)=nf(n)=n 时表示先手必败，于是我们可以抛弃掉第一次只能取 <n<n 个石子的限制。
稍微手推一下，我们应该有 f(1)=1,f(2)=2f(1)=1,f(2)=2 ，以及 f(3)=1f(3)=1 ，f(0)f(0) 似乎应该等于 00，但我们将在下文具体讨论。
根据问题一的讨论，我们应用这样一个式子来描述先后手取石子的过程：
f(n)=min⁡{i∈[1,n]∣f(n−i)>i}f(n) = \min \{ i \in [1,n] \mid f(n-i)>i\}
这表示，我们要找到一个最小的 ii ，使得拿掉 ii 个石子后，后手在 n−in-i 的局面下必胜需要的石子数严格超过 k=1k=1 倍的先手取石子数。
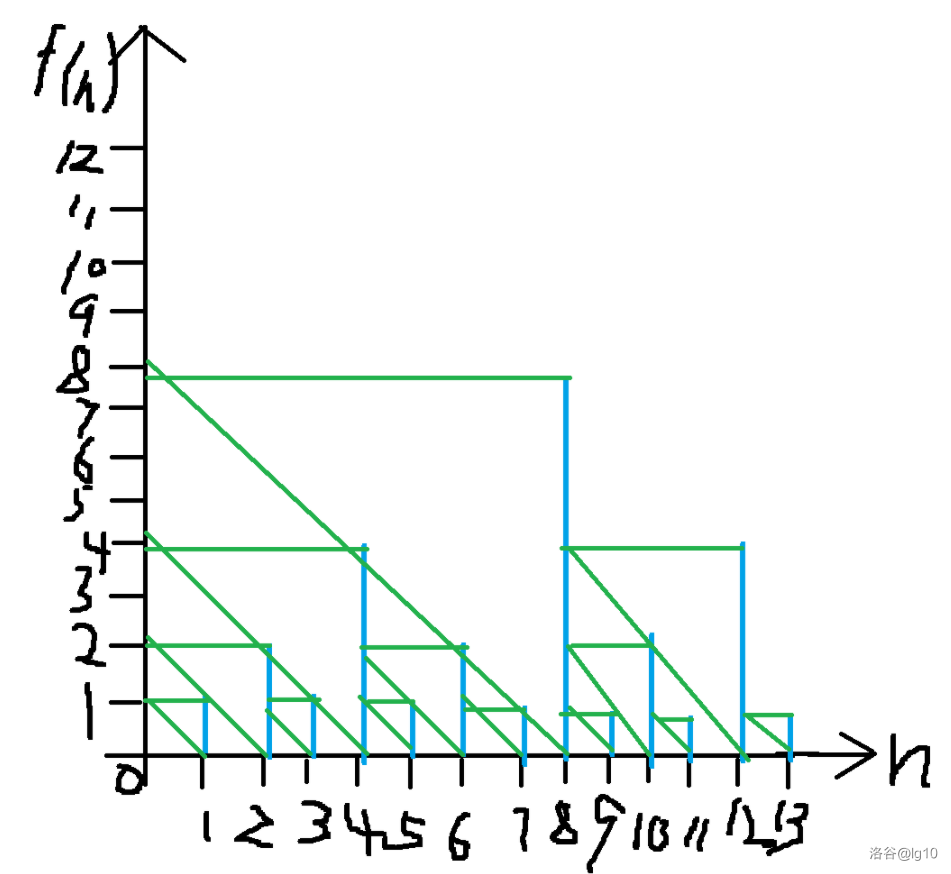
以下的所有讨论，读者均可参考下图辅助理解：
根据式子，f(0)f(0) 应该定义为 +∞+\infty。
同样地，我们把满足 f(n)=nf(n)=n 的 nn 取出组成序列 NN ，应有 N={1,2,4,8,16,...}N=\{1,2,4,8,16,...\} ，我们猜测 ff 与二进制有关，实际上可以归纳求出。
设当前已知 i∈[1,n]i \in [1,n] 的 f(i)f(i) 且 n∈Nn \in N 且当前 N={2k}N=\{2^k\} ，对于 i∈(n,n+n2]i \in (n,n+\frac{n}{2}] 的点，根据递推式一定有 f(i)<nf(i)<n ，那么这与 (0,n2](0,\frac{n}{2}] 的结构本质相同，即对于 ∀i∈(n,n+n2],f(i)=f(i−n)\forall i \in (n,n+\frac{n}{2}],f(i) = f(i-n)。
同理，对于 i∈(n+n2,n+n2+n4]i \in (n+\frac{n}{2},n+\frac{n}{2}+\frac{n}{4}] ，有 f(i)<n+n2f(i)<n+\frac{n}{2} ，与 (0,n4](0,\frac{n}{4}] 本质相同，f(i)=f(i−n−n2)f(i)=f(i-n-\frac{n}{2})。
如此递归下去，直到 n2k=1\frac{n}{2^k}=1 ，我们可以得到 ∀i∈(n,2n),f(i)=f(i−n)\forall i \in (n,2n),f(i)=f(i-n) ，而 f(2n)=2nf(2n)=2n ，即 2n∈N2n \in N。
再根据初始 f(1)=1,1∈Nf(1)=1,1 \in N ，那么一定有 N={1,2,4,8,16,32,...},f(n)=lowbit⁡(n)N = \{1,2,4,8,16,32,...\} ,f(n)=\operatorname{lowbit}(n) ，lowbit⁡(n)\operatorname{lowbit}(n) 指 nn 在二进制下最低一位的权值。
有策略后我们也可反向证明策略的正确性，即将 nn 按二进制分解后先手取走 lowbit⁡(n)\operatorname{lowbit}(n) ，此时后手只能取走 ≤lowbit⁡(n)\le \operatorname{lowbit}(n) 的值，而在后手取走后一定又会生成一个新的 lowbit⁡\operatorname{lowbit} ，且一定能被取走。
而当 n=2kn=2^k 时，由于先手无法取完，因此后手按照上述策略即可必胜，即先手必败。
即必胜策略为先手每次取走 f(n)f(n)。

2. k=2k=2

此时我们的递推式变为 f(n)=min⁡{i∈[1,n]∣f(n−i)>2i}f(n) = \min \{ i \in [1,n] \mid f(n-i)>2i\}。
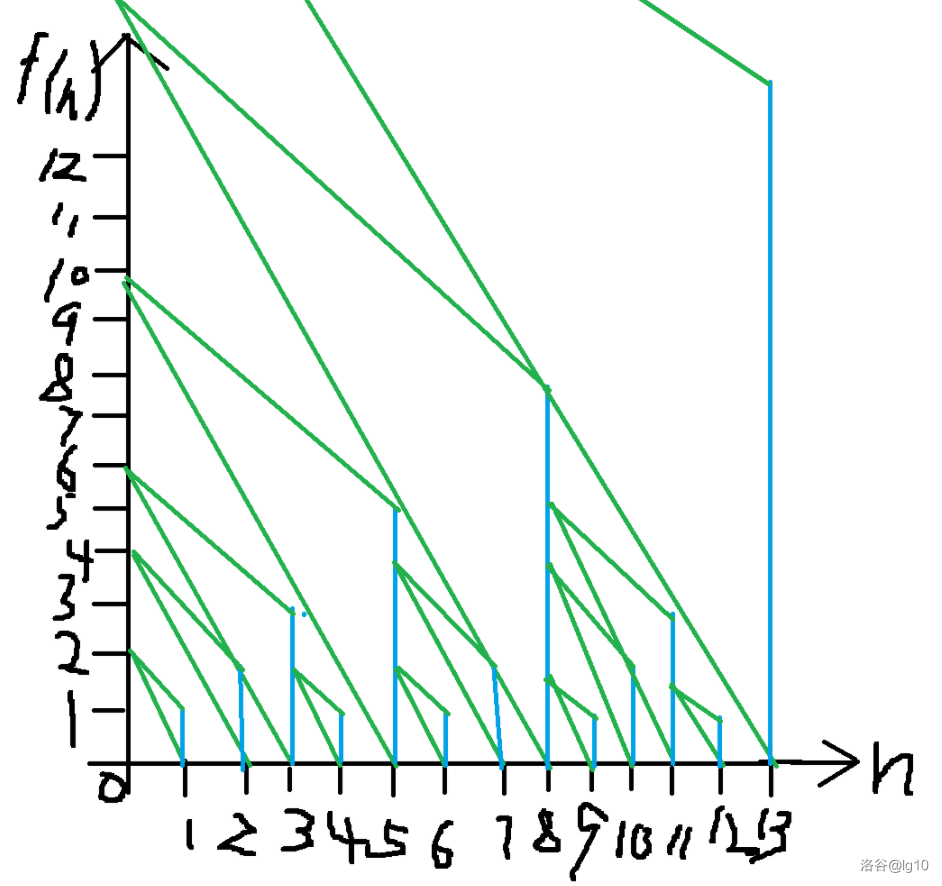
图为（画得太丑了请见谅 orz ）：
而 N={1,2,3,5,8,...}N = \{1,2,3,5,8,...\} ，我们猜测是 Fibonacci\text{Fibonacci} 数列，这也可以归纳证明。
设当前已知 i∈[1,n]i \in [1,n] 的 f(i)f(i) 且 n∈Nn \in N 且 N=FibN=\text{Fib} ，记 pre(n)=max⁡{x∈N∣2x<n},pre′(n)=min⁡{x∈N∣2x≥n}pre(n) = \max\{ x \in N \mid 2x < n \},pre'(n) = \min\{ x \in N \mid 2x \ge n \}。
我们知道 2pre(n)<n,2pre′(n)≥n2pre(n)<n,2pre'(n) \ge n，对于 i∈(n,n+pre(n)]i \in (n,n+pre(n)] 的点，根据递推式一定有 f(i)<nf(i)<n ，那么这与 (0,pre(n)](0,pre(n)] 的结构本质相同，即 ∀i∈(n,n+pre(n)],f(i)=f(i−n)\forall i \in (n,n+pre(n)],f(i) = f(i-n)。
同理，对于 i∈(n+pre(n),n+pre(n)+pre(pre(n))]i \in (n+pre(n),n+pre(n)+pre(pre(n))] ，有 f(i)<n+pre(n)f(i)<n+pre(n) ，与 (0,pre(pre(n))](0,pre(pre(n))] 本质相同，f(i)=f(i−n−pre(n))f(i)=f(i-n-pre(n))。
如此递归下去，直到 prec(n)≤2pre^c(n) \le 2 ，由 Fib\text{Fib} 的性质我们知道 1+∑i=1cprei(n)=pre′(n)1+\sum_{i=1}^c pre^i(n)=pre'(n) ，可以得到 ∀i∈(n,n+pre′(n)),f(i)=f(i−n)\forall i \in (n,n+pre'(n)),f(i)=f(i-n) ，而 f(n+pre′(n))=n+pre′(n)f(n+pre'(n))=n+pre'(n) ，即 n+pre′(n)∈Nn+pre'(n) \in N。
再根据初始 f(1)=1,f(2)=2,N={1,2}f(1)=1,f(2)=2,N=\{1,2\} ，那么一定有 N={1,2,3,5,8,13,21,...},f(n)=lowbit⁡(n)N = \{1,2,3,5,8,13,21,...\} ,f(n)=\operatorname{lowbit}(n) ，lowbit⁡(n)\operatorname{lowbit}(n) 指 nn 在 Fib\text{Fib} 进制下最低一位的权值。

3. k≥1k \ge 1

此时递推式为 f(n)=min⁡{i∈[1,n]∣f(n−i)>ki}f(n) = \min \{ i \in [1,n] \mid f(n-i) > ki\}。
初始有 N=[1,k]∩NN = [1,k] \cap \N ，我们从 ⌊k⌋+1\lfloor k \rfloor+1 开始枚举每个数，检查是否放入 NN 中。
记当前数为 xx ，类似 Fib\text{Fib} 进制的，我们把 xx 按当前 NN 中的数进行分解，记 xix_i 是分解出的从大到小第 ii 个数，为了使先手取到 lowbit⁡(x)\operatorname{lowbit}(x) 后后手一定取不到 lowbit⁡(x′)\operatorname{lowbit}(x') ，我们需要保证 xi>kxi−1x_i > kx_{i-1} ，如果不存在这样的分解就把 xx 加入集合 NN。
显然，这样得到的 NN 满足上述归纳过程的所有性质，也满足 f(n)=lowbit(n)⁡f(n) = \operatorname{lowbit(n)}。
实际上，NN 还有另外一种生成方式，一样初始为 [1,k][1,k] ，每次 N←N∪{max⁡(N)+pre′(max⁡(N))}N \leftarrow N \cup \{\max(N) + pre'(\max(N))\}，读者同样可类比 Fib\text{Fib} 进制。
同时 {x∈N∣x≤n}\{ x \in N \mid x \le n\} 的集合大小为 O(log⁡n)O(\log n) 级别。
由于笔者很菜，以上性质这里暂不给出证明 orz。

评论

共 5 条评论，欢迎与作者交流。

正在加载评论...